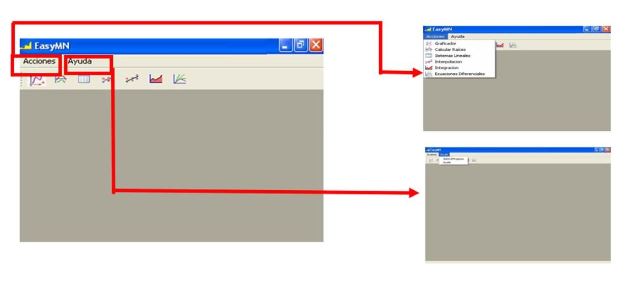
Easymn 1.1: Herramienta digital para la matemática numérica en la carrera de Ingeniería Industrial
Contenido principal del artículo
Resumen
En la carrera de Ingeniería Industrial de la UNAH ¨Fructuoso Rodríguez Pérez¨ se imparte la asignatura Matemática Numérica. En esta se hace básico en las clases prácticas resolver problemas matemáticos a través de métodos numéricos. Por lo que se hace necesario emplear un software diseñado para la enseñanza de estos contenidos. El EasyMN 1.1 constituye una herramienta digital que ha tenido un impacto en esta carrera técnica cuyo perfil no está orientado directamente hacia la programación informática. Los usuarios han expresado satisfacción por las facilidades y ventajas que proporciona en la solución de problemas, resultando motivador su empleo por ser agradable el ambiente, y fácil su manejo en las clases. En su tratamiento se tuvo en cuenta los contenidos impartidos en las asignaturas afines a la matemática que se recibe en las carreras técnicas de la Universidad cubana. A partir del programa de migración al software libre propuesto en Cuba, se confeccionó este software elaborado en plataformas libres y con código abierto como contribución a esta política a seguir.
Detalles del artículo

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.
Aquellos autores/as que tengan publicaciones con esta revista, aceptan los términos siguientes:
- Los autores/as conservarán sus derechos de autor y garantizarán a la revista el derecho de primera publicación de su obra, el cuál estará simultáneamente sujeto a la Licencia de reconocimiento-no comercial de Creative Commons 4.0 que permite a terceros compartir la obra siempre que se indique su autor y su primera publicación esta revista. Bajo esta licencia el autor será libre de:
- Compartir — copiar y redistribuir el material en cualquier medio o formato
- Adaptar — remezclar, transformar y crear a partir del material
- El licenciador no puede revocar estas libertades mientras cumpla con los términos de la licencia
Bajo las siguientes condiciones:
- Reconocimiento — Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.
- NoComercial — No puede utilizar el material para una finalidad comercial.
- No hay restricciones adicionales — No puede aplicar términos legales o medidas tecnológicas que legalmente restrinjan realizar aquello que la licencia permite.
- Los autores/as podrán adoptar otros acuerdos de licencia no exclusiva de distribución de la versión de la obra publicada (p. ej.: depositarla en un archivo telemático institucional o publicarla en un volumen monográfico) siempre que se indique la publicación inicial en esta revista.
- Se permite y recomienda a los autores/as difundir su obra a través de Internet (p. ej.: en archivos telemáticos institucionales o en su página web) antes y durante el proceso de envío, lo cual puede producir intercambios interesantes y aumentar las citas de la obra publicada. (Véase El efecto del acceso abierto).
Citas
Álvarez, M. (2007). Matemática Numérica La Habana: Editorial Félix Varela. Disponible en: http://www.slideplayer.es
Ministerio de Educación Superior. MES. (2020). Programa de la Asignatura Matemática Numérica (Carrera Ingeniería Industrial). La Habana.
Galantai, A. (2000). The Theory of Newthon's Method. Journal of Computational and Applied Mathematics , 25 - 44. Disponible en: https://www.doi.org/10.1016/S0377(00)00435-0
Hoffman, J. D. (2001). Numerical Methods for Engineer and Scientists New York: Marcel Dekker, Inc.
Press, W. H., Vetterleng, W. T., Temkolsky, S. (2002). Numerical Recipes In C. New York: Cambridge University Press. Disponible en: https://iberlibro.com y http://www.scirncedirect.com
Shampine, L. F., Allen, R. C., Pruess, S. (1997). Fundamentals of Numerical Computing. New York: John Wiley Inc.
Yamamoto, T. (2000). Historical developments in convergence analysis for Newton's and Newton-like methods . Journal of Computational and Applied Mathematics , 1 - 23.