REVIEW

  

http://opn.to/a/xisqZ

Statistical-Mathematical Modeling in Agrarian Processes. An application in Agricultural Engineering

Dr.C. Lucía Fernández-Chuairey [1] [*]

MSc. Lazara Rangel-Montes de Oca [1]

Dr.C. Caridad Walkiria Guerra-Bustillo [1]

Dr. MVZ Jany del Pozo-Fernández [1]

 

[1] Universidad Agraria de La Habana, San José de las Lajas, Mayabeque, Cuba.

  [*] Author for correspondence: Lucía Fernández-Chuairey, E-mail: lucia@unah.edu.cu

ABSTRACT

In the agrarian sector, there is an ever-growing demand to describe processes that require Statistical-Mathematical Modeling, as well as work methodologies that allow the efficient development of research projects. In this sense, the Agrarian University of Havana (UNAH) has multidisciplinary groups that develop the use of Mathematical Models, statistical tools and the use of differential calculus in search of optimal solutions and productions. Due to the interest of this topic and its repercussion in the research, the present review was developed to establish criteria and assessments in the analysis and application of models that describe Agrarian Processes, on a mathematical - statistical basis. It includes an application in studies of post-harvest curves for the weight loss (g) in pineapple crop. In addition, the Logistics and VonBertalaffy models were tested and a comparative analysis in which the Logistic Model allowed a better description and explanation of the kinetics of weight loss as well as indicators of the speed and moment, where the maximum speed of weight loss was reached. It is concluded that the development of Statistical-Mathematical Modeling allows responding to several current problems of research in the agricultural sector and to the teaching and scientific-research challenges of the new University.

Keywords: 

Mathematical modeling; agrarian processes; post-harvest curves; pineapple cultivation.

 

INTRODUCTION

Historically, the study of the dynamics of agrarian processes has been accompanied by algebraic expressions, but because they are very complex systems by nature, at first they could not be solved by the traditional methods of Mathematical Analysis. In practice, these phenomena have evolved, and in many cases, they were represented through Mathematical Statistical Models, which allow describing processes, perform detailed quantitative analyses, predict the behavior of objects in different conditions, and develop techniques that allow establishing work strategies to achieve optimal solutions and productions.

Statistical-Mathematical Modeling and its applications in Agrarian Sciences, have been present for more than 40 years at the Agrarian University of Havana and researching in collaboration with Institute of Animal Science (ICA), National Center for Agricultural Health (CENSA) and National Institute of Agricultural Sciences (INCA). They have worked biometry and modeling of agrarian and biological processes. This is corroborated in the works of Menchaca (1978, 1990), in studies of lactation curves in dairy cows, in which he used a multiplicative model with effects of these curves, in parallel. Guerra (1980), used the Response Surface Methodology (MSR) in crops of sugarcane, citrus fruits, pastures and fodder, to explore the optimal conditions of fertilization.

Menchaca (1990), used models called staged or by steps, to describe animal growth curves, and in the work of Del Pozo and Herrera (1995), the use of multiplicative models with control of growth curves and environmental effects in star grass (Cynodon nlemfumsis) growth studies is reported.

Fernández (1996, 2004), conducted a study associated with Mathematical Models that describe the dynamics of biological processes in agricultural sciences, with emphasis on nonlinear regressions and the use of iterative methods for the estimation of parameters and not by the linearization of the model as it had traditionally been worked. The development of computer science and statistical softwares facilitated the work of non-linear regressions in this way. More recently, Fernández et al. (2018), exposed the evolution in nonlinear regressions and the proposal of initial parameters from mathematical-biological interpretations of them; she also reported examples ranging from animal and plant growth models, allometric growth and lactation curves, among other processes.

Likewise, models associated with genetic evaluations and improvements in cattle (with the use of the BLUP (Best Linear Unbiased Predictor) and the use of weighing in the control day), as well as pasture growth models (King Grass) have been approached for the determination of the optimum cutting moment (Rodríguez, 2015). Other researches in the area of Agricultural Sciences have been reported by Fernández (1996a, 1996b, 2004), Del Valle (2000), Del Valle and Guerra (2012) and Vázquez et al. (2014), among others.

In Agricultural Technical Sciences, Mathematical Modeling has been applied to the prediction of quality properties of Rangel fruits (2015), in which linear and non-linear models are involved in the characterization of these processes. The theoretical basis of the most used models are addressed in this work. For the interest of this topic and its impact on research, the present review was developed to establish criteria and assessments in the analysis and application of models that describe agrarian processes, on mathematical - statistical bases.

METHODS

Theoretical fundament

The best-known case of Mathematical Models is the linear model, which is expressed in a general way as:

Yi=β0+β1x1i+β2x2i+.........+βixpi+ei  

Where:

Yi

- Dependent variable or response.

ßj

- Parameters of the model (j = 0,1,2 ... p)

x ji

- i-th value of the independent variable (j = 1,2,3, ..., p).

ei

- independent random error, with normal distribution with zero mean and variance σ2

The concept of linearity and non-linearity is referred to the parameters. In this case, (x) is considered as a constant, and the dependence of (Y) with the parameters is a combination of addition and subtraction. Menchaca (1990), when referring to linear models, points out that they present limitations from the practical and biological points of view, but they are extremely useful if the objective corresponds more to the field of estimation than to biological interpretation. In addition, these are very used by the simple mathematical method they utilize to estimate their parameters (method of ordinary least squares), which is accurate, and the solution is unique.

The general model can be taken to specific forms. Some of them are the first order polynomial, second order polynomial, and the like. Among the linear models that have shown good level of adjustment in applications within agricultural technical sciences, the cubic and polynomial logarithmic polynomial can be mentioned, whose fundamental characteristics and functional form are shown in Table 1.

TABLE 1. 

Summary of useful aspects of linear models

ModelFunctional FormFirst DerivativeInflection Point
1
Yi=β0+β1xi+β2xi2+β3xi3+ei
Yi´=β1+2β2xi+3β3xi2
x=−β2 3β3  ​ s iβ2β3 〈 0
2
y=β0+β1x+β2x2+β3ln(x)+ei
y´=β1+2β2x+β3x
x=β32β2 s iβ32β2 〉 0

1- Cubic polynomial 2-polynomial logarithmic

Yi- Dependent variable.

ßj - Parameters of the model (j = 0,1,2, ..., p)

xi - i-th value of the independent variable.

ei - independent random error, with normal distribution, with zero mean and variance σ2

Although linear models are suitable for many situations, some variables are not connected to each other by a simple relationship, such as the algebraic representation of the growth dynamics of individuals in animal species or the kinetics of postharvest weight loss. This has led to the search and construction of mathematical models, which have turned out to be non-linear in many cases.

The disadvantage of these models is that for the calculation of their parameters, iterative methods are used, and this leads to very complex calculations and can even fall into errors when estimating the parameters. Many authors use transformations to linearize the model and apply the minimum method square, but in practice, this procedure is not advisable. At present, there are specific programs for non-linear adjustment, which allow overcoming this disadvantage.

Within the non-linear models frequently used are those that are asymptotic without inflection points (Models of Brody, Modified Exponential) and those that are asymptotic with inflection points (Models of Gompertz, Von-Bertalanffy, and Logistic, among others). Table 2 shows the algebraic expressions of some of these models, as well as indicators associated with the calculation of speed and / or the rate of profit (first derivative), point of inflection.

TABLE 2. 

Functional form and aspects related to non-linear models

Brody ModelLogistic ModelVon Bertalanffy Model
Functional form
f(t)=A(1−be−kt)
f(t)=A(1+be−kt)
f(t)=A(1−be−kt)3
DescriptionAsymptotic model without inflection point Asymptotic model with inflection point Asymptotic model with inflection point
Asymptote AAA
Profit rate or first rate
f′(t)=Abke−kt
f′(t)=Abke−kt(1+be−kt)2
f′(t)=3A(1−be−kt)2bke−kt
Second derivative features
f″(t)=−Ak2be−kt
f″(t)=Abk2e−kt(be−kt−1)(1+be−kt)3
f″(t)=3Abke−kt(1-be−kt)2+  2(3Abe−kt(1−be−kt)(bke−kt))
Inflection point-
t=lnbk
t=ln 3bk

f (t): Dependent random variable, t: Independent variable, controlled or predefined, A, b, k: parameters to be estimated.

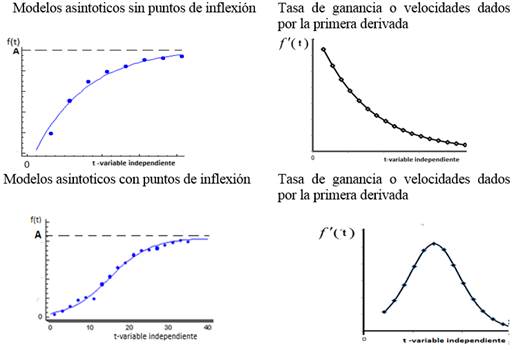
In the Brody model, the function is concave and grows until its value stabilizes as the value of t increases; however, the velocities or rates (f l (x)) decrease as the value of t increases. (Figure 1)

The shape of the rest of the models is sigmoid. The difference between them is the location of the inflection point. The speeds or rates in these models is flared; this increases until it reaches its maximum value, and then decreases to zero. (Figure 1)

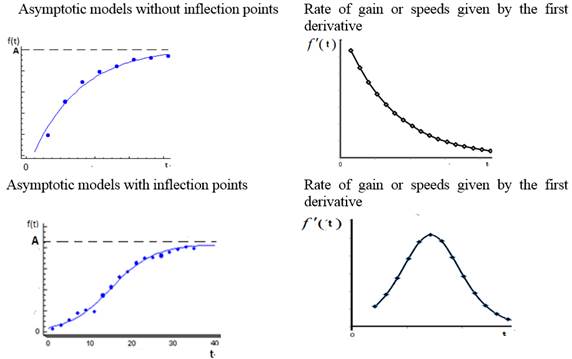
2071-0054-rcta-28-02-e08-gf1.jpg

FIGURE 1. 

Representation of non-linear models and their corresponding rates or speeds.

Application of These Models in Studies of Post-Harvest Curves of Pineapple (variety Cayena Lisa)

The study was carried out in areas of the company of several crops located within the Havana-Matanzas Plain, with a range of average annual temperature between 25 and 32 ºC and high humidity. Weight Loss (PP) was performed through the weighing of fruits with the use of the electronic balance, during the first nine days after harvesting. Average values (g) were calculated on the days observed. The Logistics and Von Vertalanffy models (described above) were tested. For the goodness of fit and discrimination between models, the coefficient of determination, sum of the square of the error, significance of the model and the parameters, distribution of the residuals and Durbin Watson's hypothesis test were taken into account. The loss process is described from the best model. The speed with which the weight loss occurs at each instant of the period analyzed is estimated from the derivative of the function, and the search of the moment where the maximum speed of weight loss occurred was calculated by the inflection point.

RESULTS OBTAINED

The average values of weight loss (g) and the corresponding days allowed us to estimate the parameters of the adjusted curves (Table 3), which showed good adjustment with coefficient of determination above 97%. This indicates that both models are an alternative for the description of the process and for the prediction within the range of values studied.

The discrimination between the models allowed selecting the Logistic Model as the best one, which explains 99.27% of the total variability. All its parameters are significant and it achieved lower standard error of estimation, absolute mean of the error and sum of squared of the error than the model of Von - Bertalaffy (Table 3).

TABLE 3. 

Result of the adjustment of the models

Logistic ModelVon-Betallanffy Model
Coefficient of Determination (R2) %99.27%97.64%
Significance of the model significantsignificant
Adjusted model (estimated parameters)
f(t)=4.57(1+36.25e−0.93 t)
f(t)=4.98 (1−1.12 e−0.43 t)3
Significance of the parametersAll significantAll significant
Standard estimation error 0.200.36
Sum of error square0.160.52
Durbin Watson2.382.19

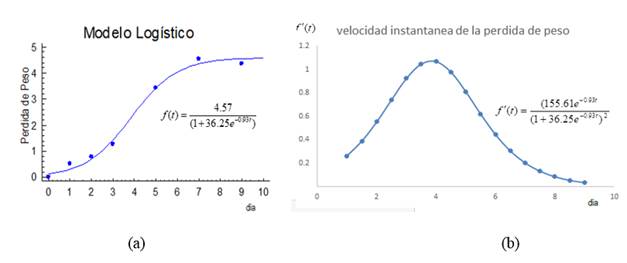
The Logistic model selected (Figure 2a) shows the increase in weight loss as the post-harvest day’s increase, with abrupt behavior during the first days and a tendency to stabilize this value from the seventh day. This trend described by the model is considered adequate and is associated, among other aspects, with the irreversible physiological changes that occur in the fruit.

Another indicator of interest is associated to the behavior of the speed with which this weight loss occurs (Figure 2b), which is in flared form. This increases until reaching its maximum value, approximately on the fourth day, and then decreases to zero.

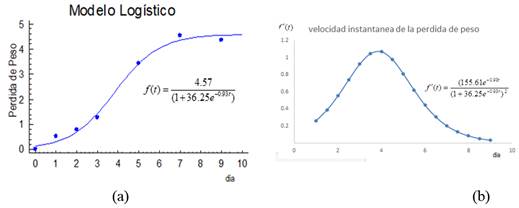
2071-0054-rcta-28-02-e08-gf2.jpg

FIGURE 2. 

Model of best fit for weight loss (2a) and speed with which it occurs (2b).

Table 4 shows the inflection point (3.8, 2.24) which is where the maximum speed of weight loss is reached. It was of 1.07 g. It also shows the values reached around this point.

TABLE 4. 

Behavior of the weight loss and the speed with which the weight loss occurs around the inflection point

Day3.53.63.73.83.944.14.2
Weight Lossing (g)1.9272.0322.1382.2452.3522.4592.5652.669
Speed of PP (g)1.0461.0601.0681.0731.0721.0671.0581.044

These indicators associated with the loss of weight, are of special interest to save resources, time and efforts, which allows tracing postharvest handling strategies and guarantee the quality of the product.

Currently, there are valuable results regarding the use of these and other types of models that have been used to predict the production of green and dry grass biomass (Maralfalfa). They have been studied with several doses of nitrogen fertilizer; or in the description and characterization of the physical and chemical properties of the pineapple (variety Cayenne Lisa) stored at room temperature. Moreover, they have been used in the modeling and simulation of the star grass (C. nlemfuensis) performance under different management conditions and climatic scenarios (Fernández et al., 2011; Rangel, 2015; López, 2016 and others).

CONCLUSIONS

  • To deal in detail with the analysis of agrarian processes, knowledge of a group of models is required with the application of Differential Calculus and Mathematical Statistics, among other aspects.

  • The graph of different models, as well as their absolute rates, help to clarify the analysis of the dynamics of different agrarian phenomena.

  • Mathematical modeling allows deepening the laws that govern each of the phenomena, facilitates the study of the process and creates a methodological basis for the processing of information

  • It is concluded that the development of Statistical-Mathematical Modeling allows responding to current problems of research in the agricultural sector and to the teaching and scientific-research challenges of the new University.

REFERENCES

DEL POZO, P.P.; HERRERA, R.S.: “Modelado del crecimiento del pasto estrella (Cynodon nlemfuensis). 1. Modelo multiplicativo con control de la curva de crecimiento y los efectos ambientales”, Pastos y Forrajes, 18(2): 171, 1995, ISSN: 0864-0394.

DEL VALLE, J.: La Multicolinealidad en Modelos de Regresión Lineal Múltiple. Propuesta de solución, Universidad Agraria de La Habana (UNAH), PhD Thesis, San José de las Lajas, La Habana, Cuba, 2000.

DEL VALLE, M.J.; GUERRA, B.W.: “La multicolinealidad en modelos de regresión lineal múltiple”, Revista Ciencias Técnicas Agropecuarias, 21(4): 80-83, 2012, ISSN: 1010-2760, E-ISSN: 2071-0054.

FERNÁNDEZ, C.L.; GUERRA, B.C.W.; DE CALZADILLA, P.J.; CHANG, L.N.U.: “Desarrollo de la modelación estadístico-matemática en las ciencias agrarias. Retos y perspectivas”, Investigación Operacional, 38(5): 462-467, 2018.

FERNÁNDEZ, L.: Modelos que describen la dinámica de los procesos biológicos en las ciencias, Universidad Agraria de La Habana, Cuba, MSc. Thesis, San José de las Lajas, La Habana, Cuba, 60 p., 1996a.

FERNÁNDEZ, L.: “Modelos que describen la dinámica de los procesos biológicos en las Ciencias Agropecuarias”, La Habana, Cuba: Universidad Agraria de la Habana, 1996b.

FERNÁNDEZ, L.: Modelos estadísticos-matemáticos en el análisis de la curva de lactancia y factores que la afectan en el genotipo Siboney de Cuba, Universidad Agraria de La Habana, Instituto de Ciencia Animal, Veterinary Doctor Thesis., San José de las Lajas, La Habana, Cuba, 100 p., 2004.

FERNÁNDEZ, L.; TONHATI, H.; ALBUQUERQUE, L.G.; ASPILCUETA-BORQUIS, R.R.; MENÉNDEZ BUXADERA, A.: “Modelos de regresiones aleatorias para la estimación de parámetros genéticos y estudios de curvas de lactancia del Holstein en Cuba”, Revista Cubana de Ciencia Agrícola, 45(1), 2011, ISSN: 0034-7485.

GUERRA, B.C.W.: Relación Modelo-Diseño de tratamientos en la determinación de las dosis óptimas de fertilizantes con experimentos de Campo en Cuba, Instituto de Suelos y Agroquímica ¨Nikola Pushkarov¨, PhD. Thesis, Sofía, Bulgaria, 184 p., 1980.

LÓPEZ, J.L.: Modelación y simulación del rendimiento del pasto estrella (C. nlemfuensis) bajo diferentes condiciones de manejo y escenarios climáticos, Universidad Agraria de La Habana, Cuba, MSc. Thesis, San José de las Lajas, Mayabeque, Cuba, 79 p., 2016.

MENCHACA, M.A.: Modelo multiplicativo. Efecto de curva de lactancia controlado para el análisis estadístico de experimentos con vacas lecheras, Instituto Suoerior de Ciencias Agropecuarias-Instituto de Ciencia Animal, PhD Thesis, San José de las Lajas, La Habana, Cuba, 1978.

MENCHACA, M.A.: “El uso de modelos etápicos para describir las curvas de crecimiento animal”, Revista Cubana Ciencias Agrícolas, 24(1): 29-34, 1990, ISSN: 0034-7485.

RANGEL, M.L.: Variabilidad temporal de las propiedades físicas, químicas y mecánicas de la piña, variedad Cayena Lisa, almacenada a temperatura ambiente, Universidad Agraria de La Habana, Cuba, MSc. Thesis, San José de las Lajas, Mayabeque, Cuba, 99 p., 2015.

RODRÍGUEZ, L.: Modelación y simulación de la producción de biomasa de Pennisetum purpureum Schum vc. King Grass y su aplicación en la alimentación animal, Universidad Agraria de La Habana, PhD Thesis, San José de las Lajas, Mayabeque, Cuba, 2015.

VÁZQUEZ, A.Y.; GUERRA, B.C.W.; SÁNCHEZ, L.O.E.: “Modelación estadístico-computacional para el estudio de la sostenibilidad socioeconómica de la empresa pecuaria Valle del Perú”, Investigación Operacional, 35(2): 121-130, 2014.

 

 

Received: 25/07/2018

Accepted: 25/02/2019

 

 

Lucía Fernández-Chuairey, Profesor Titular, Universidad Agraria de La Habana (UNAH), Departamento de Matemática y Física, e-mail: lucia@unah.edu.cu

Lazara Rangel-Montes de Oca . , Profesor Asistente, (UNAH), Departamento de Ingeniería Agrícola, e-mail: lazarar@unah.edu.cu

Caridad Walkiria Guerra-Bustillo, Profesor Titular, (UNAH), Departamento de Matemática y Física, e-mail: luzmi@infomed.sld.cu

Jany del Pozo-Fernández. Adiestrada, Facultad de Medicina Veterinaria, e-mail: janydelpozo@gmail.com

The authors of this work declare no conflict of interest.

This article is under license Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)  

 

REVISIÓN

 

Modelación Estadístico-Matemática en Procesos Agrarios. Una aplicación en la Ingeniería Agrícola

Dr.C. Lucía Fernández-Chuairey [1]

MSc. Lazara Rangel-Montes de Oca [1]

Dr.C. Caridad Walkiria Guerra-Bustillo [1]

Dr. MVZ Jany del Pozo-Fernández [1]

[1] Universidad Agraria de La Habana, San José de las Lajas, Mayabeque, Cuba.

  [*] Autor para correspondencia: Lucía Fernández-Chuairey, E-mail: lucia@unah.edu.cu

RESUMEN

En el sector agrario existe una demanda siempre creciente de describir procesos que requieren de la Modelación Estadístico-Matemática, así como de metodologías de trabajo que permitan el desarrollo eficiente de los proyectos de investigación. En tal sentido la Universidad Agraria de La Habana (UNAH) cuenta con grupos multidisciplinarios que desarrollan el uso de Modelos Matemáticos, herramientas estadísticas y el empleo del cálculo diferencial en busca de soluciones y producciones óptimas. Por el interés de esta temática y su repercusión en la investigación, se desarrolló la presente revisión para establecer criterios y valoraciones en el análisis y aplicación de modelos que describen Procesos Agrarios, sobre bases matemático - estadísticas. Se incluye una aplicación en estudios de curvas pos cosecha para la perdida de peso (g) en el cultivo de la Piña, se probaron los Modelos Logístico y Von Bertalaffy y se realiza un análisis comparativo en el que el Modelo Logístico permitió mejor descripción y explicación de la cinética de pérdida de peso e indicadores de la velocidad y momento donde se alcanzó la máxima velocidad de pérdida de peso. Se concluye que el desarrollo de la Modelación Estadístico-Matemática, permite dar respuesta a diversos problemas vigentes de investigación en el sector agrario y a retos docentes y científico-investigativo de la nueva Universidad.

Palabras clave: 

modelación matemática; procesos agrarios; curvas poscosecha; cultivo de piña.

INTRODUCCIÓN

Históricamente el estudio de la dinámica de procesos agrarios ha ido acompañada de expresiones algebraicas, pero por ser sistemas muy complejos por naturaleza, en un inicio no pudieron ser resueltos por los métodos tradicionales del Análisis Matemático. En la práctica estos fenómenos han evolucionado y en muchos casos se representaron a través de Modelos Estadísticos Matemáticos, los que permiten describir procesos, realizar análisis cuantitativos detallados, predecir el comportamiento de los objetos en diversas condiciones y desarrollar técnicas que permiten establecer estrategias de trabajo para lograr soluciones y producciones óptimas.

La Modelación Estadístico-Matemática y sus aplicaciones en las Ciencias Agrarias, ha estado presente por más de 40 años en la Universidad Agraria de La Habana y en investigaciones en colaboración con el Instituto de Ciencia Animal (ICA), el Centro Nacional de Sanidad Agropecuaria (CENSA) y el Instituto Nacional de Ciencia Agrícola (INCA), en los trabajos de los especialistas biométricos y profesionales afines, que abarcan la modelación de procesos agrarios, y biológicos. Lo cual se corrobora en los trabajos de Menchaca (1978, 1990), en estudios de curvas de lactancia en vacas lecheras donde utilizó un modelo multiplicativo con efectos de estas curvas, paralelamente Guerra (1980), empleó la Metodología de Superficie de Respuesta (MSR) en los cultivos de la caña de azúcar, cítricos, pastos y forrajes, para explorar las condiciones óptimas de fertilización.

Menchaca, (1990), usó modelos a los que denomino etápicos, para describir curvas de crecimiento animal y en el trabajo de Del Pozo y Herrera (1995), se divulga el empleo de modelos multiplicativos con control de curvas de crecimiento y efectos ambientales en estudios de crecimiento del pasto estrella (Cynodon nlemfumsis).

Fernández (1996, 2004), realiza un estudio asociado a Modelos Matemáticos que describen la dinámica de los procesos biológicos en las Ciencias Agropecuarias, con énfasis en regresiones no lineales y el empleo de métodos iterativos para la estimación de los parámetros y no mediante la linealización del modelo como tradicionalmente se venía trabajando, donde el propio desarrollo de la informática y de los software estadístico facilitó trabajar las regresiones no lineales por esta vía. Más reciente Fernández et al. (2018), exponen la evolución en regresiones no lineales y la propuesta de parámetros iniciales a partir de interpretaciones matemático-biológicas de los mismos, reportan además ejemplos que van desde los modelos de crecimiento animal y vegetal, el crecimiento alométrico y las curvas de lactancia, entre otros procesos.

De igual forma han sido abordados modelos asociados a evaluaciones y mejoramientos genéticos en bovinos (con el empleo del BLUP ( Best Linear Unbiased Predictor) y el uso del pesaje en el día de control), así como modelos de crecimiento en pastos (King Grass) para la determinación del momento óptimo de corte abordados por Rodríguez (2015). Se alcanzan otras investigaciones en el área de las Ciencias Agropecuarias reportadas por, Fernández (1996a, 1996b, 2004); Del Valle (2000); del Valle y Guerra (2012); Vázquez et al. (2014); entre otros.

En las Ciencias Técnicas Agropecuarias la Modelación Matemática ha sido aplicada a la predicción de propiedades de calidad de los frutos Rangel (2015), donde para la caracterización de estos procesos intervienen modelos lineales y no lineales, cuya fundamentación teórica de los modelos más utilizados serán abordados en el presente trabajo. Por el interés de esta temática y su repercusión en la investigación se desarrolló el mismo, para establecer criterios y valoraciones en el análisis y aplicación de modelos que describen Procesos Agrarios, sobre bases matemático- estadísticos.

MÉTODOS

Fundamentos teóricos

El caso más conocido de Modelos Matemáticos, lo constituye el modelo lineal siendo expresado de forma general como:

Yi=β0+β1x1i+β2x2i+.........+βixpi+ei  

donde:

Yi

- Variable dependiente o respuesta.

ßj

- Parámetros del modelo (j = 0,1,2…p)

x ji

- Valor i-esimo de la variable independiente (j =1,2,3,…,p).

ei

- error aleatorio independiente, con distribución normal con media cero y varianza (2.

El concepto de linealidad y no linealidad está referida a los parámetros, en este caso se considera (x) como una constante y la dependencia de (Y) con los parámetros es una combinación de sumas y restas. Menchaca (1990), al referirse a modelos lineales señala que presentan limitaciones desde el punto de vista práctico y biológico, pero son sumamente útiles si el objetivo corresponde más al campo de la estimación que a la interpretación biológica. Además estos son muy utilizados por lo simple del método matemáticos que utiliza para estimar sus parámetros (método de los mínimos cuadrados ordinarios), el cual es exacto y la solución es única.

El modelo general puede ser llevado a formas específicas siendo alguna de ellos el polinomial de primer orden, polinomial de segundo orden, etc. De los modelos lineales que han mostrado buen nivel de ajuste en aplicaciones dentro de las ciencias técnicas agropecuarias se tiene el polinomial cúbico y polinomial logarítmico, cuyas características fundamentales y forma funcional se muestran en la Tabla 1.

TABLA 1. 

Resumen de aspectos útiles de modelos lineales

ModeloForma funcionalPrimera derivadaPunto de inflexión
1
Yi=β0+β1xi+β2xi2+β3xi3+ei
Yi´=β1+2β2xi+3β3xi2
x=−β2 3β3  ​ s iβ2β3 〈 0
2
y=β0+β1x+β2x2+β3ln(x)+ei
y´=β1+2β2x+β3x
x=β32β2 s iβ32β2 〉 0

1- polinomial cúbico 2-polinomial logarítmico

Yi- Variable dependiente.

ßj - Parámetros del modelo (j=0,1,2,…,p)

xi - Valor i-esimo de la variable independiente.

ei - error aleatorio independiente, con distribución normal con media cero y varianza (2.

Aunque los modelos lineales son adecuados para muchas situaciones, algunas variables no se conectan entre sí por una relación tan simple, como por ejemplo la representación algebraica de la dinámica de crecimiento de individuos en especies de animales o la cinética de pérdida de peso en postcosecha, lo que han llevado a la búsqueda y construcción de modelos matemáticos los cuales han resultado ser de características no lineales en muchos casos.

La desventaja de estos modelos es que para el cálculo de sus parámetros se utilizan métodos iterativos y esto lleva cálculos muy complejos e incluso se puede caer en errores al estimar los parámetros, muchos autores utilizan transformaciones para linealizar el modelo y aplicar el método de los mínimos cuadrados, pero en la práctica este procedimiento no es aconsejable, en la actualidad existen programas específicos para el ajuste no lineal el cual permite superar esta desventaja.

Dentro de los modelos no lineales se utilizan con frecuencia aquellos que son asintóticos sin puntos de inflexión en los que se encuentran los modelos de Brody, Exponencial Modificada y los asintóticos con puntos de inflexión dentro de estos modelos están: Gompertz, Von-Bertalanffy, Logístico, entre otros .En la Tabla 2 se muestran las expresiones algebraicas de algunos de estos modelos, así como indicadores asociadas al cálculo de velocidad y/o a tasa de ganancia (primera derivada), punto de inflexión.

TABLA 2. 

Forma funcional y aspectos relacionados con modelos no lineales

Modelo de BrodyModelo LogísticoModelo Von Bertalanffy
Forma funcional
f(t)=A(1−be−kt)
f(t)=A(1+be−kt)
f(t)=A(1−be−kt)3
DescripciónModelo asintótico sin punto de inflexiónModelo asintótico con punto de inflexiónModelo asintótico con punto de inflexión
AsíntotaAAA
Tasa de ganancia o velocidad (primera derivada)
f′(t)=Abke−kt
f′(t)=Abke−kt(1+be−kt)2
f′(t)=3A(1−be−kt)2bke−kt
Segunda derivada Características
f″(t)=−Ak2be−kt
f″(t)=Abk2e−kt(be−kt−1)(1+be−kt)3
f″(t)=3Abke−kt(1-be−kt)2+  2(3Abe−kt(1−be−kt)(bke−kt))
Punto de inflexión No tiene
t=lnbk
t=ln 3bk

f(t): Variable aleatoria dependiente, t :Variable independiente, controlada o predefinida, A,b,k: parámetros a estimar

En el modelo de Brody la función es cóncava y crece hasta estabilizar su valor a medida que aumente el valor de t, sin embargo las velocidades o tasas (f l (x)) disminuyen a medida que aumenta el valor de t. (Figura 1)

El resto de los modelos su forma es sigmoide. La diferencia entre ellos es la localización del punto de inflexión Las velocidades o tasas en estos modelos es en forma acampanada esta aumenta hasta alcanzar su máximo valor, después decrece hasta hacerse cero (Figura 1)

2071-0054-rcta-28-02-e08-gf3.jpg
f(t): Variable aleatoria dependiente, t :Variable independiente, controlada o predefinida, A-,asíntota

FIGURA 1. 

Representación de Modelos no lineales y sus correspondientes tasas o velocidades.

Ejemplo de aplicación de estos modelos en estudios de curvas pos cosecha de la Piña (variedad Cayena Lisa)

El estudio se llevó a cabo en áreas de la empresa de cultivos varios ubicada dentro de la Llanura Habana-Matanzas, con un rango de la temperatura media anual entre los 25 y los 32 ºC y elevada humedad ambiental. La Pérdida de Peso (PP) se realizó a través del pesaje de los frutos con la utilización de la balanza electrónica, durante los primeros nueve días de cosechado, se calcularon valores promedios (g) en los días observados. Se probaron los modelos Logísticos y de Von Vertalanffy (descritos anteriormente), para la bondad de ajuste y discriminación entre modelos se tuvo en cuenta el coeficiente de determinación, suma de cuadrado del error, significación del modelo y de los parámetros, distribución de los residuos y docima de Durbin Watson. Se describe el proceso de perdida a partir del mejor modelo, se estima la velocidad con que se produce la pérdida de peso en cada instante del período analizado a partir de la derivada de la función y para la búsqueda del momento donde se produjo la máxima velocidad de pérdida de peso se calculó mediante el punto de Inflexión.

RESULTADOS Y DISCUSIÓN

Los valores promedios de pérdida de peso (g) y los días correspondientes, permitieron estimar los parámetros de las curvas ajustadas (tabla 3), las que mostraron buen ajuste con coeficiente de determinación por encima del 97%. Lo que indican que ambos modelos son una alternativa para la descripción del proceso y para la predicción dentro del rango de valores estudiados.

La discriminación entre los modelos, seleccionó al Modelo Logístico como el mejor, el que logra explicar el 99.27 % de la variabilidad total, y donde todos sus parámetros son significativo y logró menores: error estándar de estimación, media absoluta del error y suma de cuadrado del error que el modelo de Von-Bertalaffy (Tabla 3).

TABLA 3. 

Resultado del ajuste de los modelos

Modelo LogísticoModelo Von-Betallanffy
Coeficiente de Determinación (R2) %99,27%97,64%
Significación del modelosignificativo significativo
Modelo ajustado (parámetros estimados)
f(t)=4,57(1+36,25e−0,93 t)
f(t)=4,98 (1−1,12 e−0,43 t)3
Significación de los parámetrosTodo significativosTodo significativos
Error estándar de estimación0,200,36
Suma de cuadrado del error0,160,52
Durbin Watson2,382,19

El modelo Logístico seleccionado (Figura 2a) muestra, el aumento de la pérdida de peso a medida que se incrementan los días postcosecha, con un comportamiento brusco los primeros días y una tendencia a estabilizar este valor a partir del séptimo día. Esta tendencia descritas por el modelo se considera adecuada y están asociadas entre otros aspectos a los cambios fisiológicos irreversibles que se suceden en la fruta.

Otro indicador de interés se asocia al comportamiento de la velocidad con que se produce esta pérdida de peso (Figura 2b), que es en forma acampanada esta aumenta hasta alcanzar su máximo valor aproximadamente en el cuarto día y después decrece hasta hacerse cero

2071-0054-rcta-28-02-e08-gf4.jpg

FIGURA 2. 

Modelo de mejor ajuste para la pérdida de peso (2a) y velocidad con que se produce la misma 2(b).

En la Tabla 4 se observa el punto de inflexión (3,8, 2,24) que es donde se alcanza la máxima velocidad de pérdida de peso, siendo este de 1,07 g, se muestra además los valores alcanzados alrededor de este punto.

TABLA 4. 

Comportamiento de la pérdida de peso y la velocidad con que se produce la pérdida de peso alrededor del punto de inflexión

Día3,53,63,73,83,944,14,2
Pérdida de Peso (g)1,9272,0322,1382,2452,3522,4592,5652,669
Velocidad de PP(g)1,0461,0601,0681,0731,0721,0671,0581,044

Estos indicadores asociados a la pérdida de peso, cobran un especial interés para economizar recursos, tiempo y esfuerzos, lo que permite trazar estrategias de manejo postcosecha y garantizar la calidad del producto.

En la actualidad se cuenta con valiosos resultados relativos al empleo de estos y otros tipos de modelos que han sido utilizado para la predicción de la producción de biomasa verde y seca del pasto (Maralfalfa) con varias dosis de fertilizante nitrogenado; o en la descripción y caracterización de las propiedades físicas y químicas de la piña (variedad cayena Lisa) almacenada a temperatura ambiente, así como en la modelación y simulación del rendimiento del pasto estrella (C. nlemfuensis) bajo diferentes condiciones de manejo y escenarios climáticos, como muestran los trabajos de Fernández et al. (2011); Rangel (2015); López (2016), entre otros autores.

CONCLUSIONES

  • Para abordar de forma detallada el análisis de procesos agrarios se requiere entre otros aspectos del conocimiento de un grupo de modelos con la aplicación del Cálculo Diferencial y la Estadística Matemática.

  • La gráfica de diferentes modelos, así como sus tasas absoluta contribuye a esclarecer los análisis sobre la dinámica de diferentes fenómenos agrarios.

  • La modelación matemática permite profundizar en las leyes que rigen cada uno de los fenómenos y facilita el estudio del proceso y crea base metodológica para el procesamiento de la información

  • El desarrollo de la Modelación Estadístico -Matemático, permite dar respuesta a problemas vigentes de investigación en el sector agrario y a los retos docentes y científico-investigativo de la nueva Universidad.