ORIGINAL ARTICLE

http://opn.to/a/2UZGg
Simulation of Clay Soil De-Compaction Using Discrete Element Method
Dr.C. Elvis López-Bravo [I] [*]
Dr.C. Engelbert Tijskens [II]
Dr.C. Omar González-Cueto [I]
Dr.C. Miguel Herrera-Suárez [I]
Dr.C. José Dasiell Lorenzo-Rojas [I]
[I] Universidad
Central de las Villas “Marta Abreu”, Facultad de Ciencias Agrícolas,
Departamento de Ingeniería Agrícola, Santa Clara, Villa Clara, Cuba.
[II] Catholic
University of Leuven, Faculty of Bioscience Engineering, Department of
Biosystems, Division of Mechatronics, Biostatistics and Sensors
(MeBioS), Kasteelpark Arenberg 30, B-3001 Heverlee, Belgium.
[*] Author for correspondence: Elvis López-Bravo, E-mail: elvislb@uclv.edu.cu
ABSTRACT
Draft
force prediction and soil mechanical behavior during soil de-compaction
was implemented by using the Discrete Element Method. The model
parameters were defined as a function of the mechanical properties a
clay soil, previously obtained by laboratory tests. The properties used
by the model are cohesion, adhesion, internal friction, external
friction, Young’s modulus and Poisson’s coefficient. The effect of the
subsoiler shape variation was simulated under dry-compacted soil
conditions, showing clear variations in forces related with the tool
geometry. Increasing in complexity of the tool geometry the simulation,
the model showed advantages in terms of demanded pressure and volume of
soil disrupted. The soil de-compaction with hardpan formation was also
simulated by introducing two different compacted soil sections in the
virtual block. The compaction level was defined by two set of
micro-particles with different density resulting from modifying the soil
dry bulk density at the model macro-parameter. The simulation shows the
feasibility of modelling separately the forces demanded for the
different part of the tillage tool and the soil particle pattern of
movement during the operation.
Keywords:
Tillage; prediction; friction; compaction; implement.
In
agricultural practices a subsoiler is a tillage tool used for working
the deep layers in the soil. It is characterised by a robust structure
and being a large power consumer. This implement was designed to fight
against compaction, however, the non-inversion capacity of the tool also
contributes to prevent erosion and soil degradation (Zheng et al., 2016; Li et al., 2017).
Hardpan
formation is commonly associated with mouldboards ploughing. To disrupt
the hardpan layer a special tillage operation of subsoiling is needed
in order to restore the soil productivity by growing water infiltration,
root development and soil aeration. Several studies have focused on
tillage force requirements aimed to optimize the tool design. They are
motivated by the need to reduce the energy consumed where the soil
physical state, the tool geometry, and the selected operational
parameters play an important role (Zheng et al., 2017).
No homogenous bulk density is generally found at the different soil
layers. Several studies have been related to the degree of densification
with the soil mineral composition, physical factors, and systematic
loading by transporting and tillage operations (Morris et al., 2010; Li et al., 2016b).
On
the other hand, numerical models have been implemented taking account
for the tool geometry, leading to numerical solutions for tillage
applications. Using Finite Element Models (FEM), several authors
reported satisfactory results related to the tool structural resistance
and tillage force demanded. These results showed the advantages of the
FEM models with regard to analytical calculations based on soil passive
pressure. FEM was found suitable for a continuum analysis under static
conditions of soil and tool interaction (Tadesse, 2004).
However, this method results unstable for modelling particle flows and
crack formation. On the contrary, the models implemented on Discrete
Element Methods (DEM) were successfully used to simulate the flow of
granular material based on the interaction of the forces among elements
in contact, describing the discontinuous dynamical behaviour of the
particles. However, only a few attempts were made when using DEM for
tillage operations (Mak et al., 2012; López, 2014; Ding et al., 2017; Hang et al., 2017).
The
present investigation aims to simulate soil subsoiling at different
levels of soil compaction using different designs of the tools in order
to predict the draft force requirements.
The dynamics of soil and tool interaction was implemented using the DEM software DEMeter++ (Tijskens et al., 2003), based on the classic model proposed by Cundall (1988).
In order to calculate the interaction between soil particles and
tillage tool, an explicit contact model was developed using the
Mohr-Coulomb criterion of soil failure. The model, at the particle
level, deals with normal force, shear force, cohesion force and friction
force. The stiffness in normal and tangential direction were calculated
based on the equation of the best fit to relate soil elastic properties
with the geometry of the particles.in contact. The soil and tool
parameters used by the model were: Young’s modulus (E), Poisson’s ratio (n), internal friction angle (f), soil-steel friction angle (d), soil cohesion (c) and adhesion (c
a
). Model formulation, calibration and validation were described
in detail on the implementation of prediction model for non-inversion
soil tillage (López, 2014).
Three-tool
designs called simple, knife and blade subsoiler were used to perform
simulations of soil de-compaction. The geometry of the tools was
increased in complexity by adding different parts to the basic
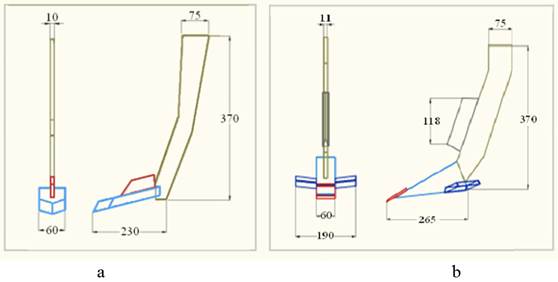
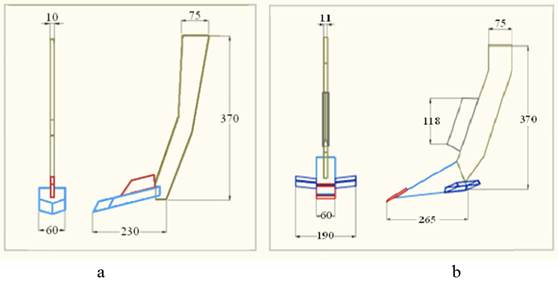
structure. Figure 1a shows the geometry of the simple subsoiler, the shape of the knife subsoiler having the same structure as the blade one (Figure 1b), but without lateral blades.
FIGURE 1.
Simple subsoiler (a), and blade subsoiler (b).
The soil block was sized at 350x350x600 mm and
particles size were divided in three sets with the average radios at
3.5, 5.0 and 7.0 mm for a total of 45 000 spherical particles.
Micro-density was the same for compacted soil block defined at w = 9 % and rd = 1.3 g/cm3. For hardpan, however, soft soil section is defined at w = 12% and rd = 1. 0 g/cm3, while harden soil section is defined at w = 12%, rd = 1.35 g/cm3.
These conditions were selected considering the variation in dry bulk
density. The mechanical properties used as model macro-parameters are
shows in Table 1. On the other hand, the
force distribution on the soil particles was generated at the maximum
depth of tillage or plowing floor; it was obtained in soft and compacted
soil conditions, according to the parameters of the model.
TABLE 1.
Soil macro-parameters
| Model Parameters | Soil conditions |
|---|
| Soft | Hardpan | Compacted | Unit |
|---|
| E | 39.0 | 81.3 | 101.86 | MPa |
| v | 0.3 | 0.4 | 0.46 | |
| C | 54.5 | 104.1 | 133.60 | kPa |
| Ca | 7.6 | 1.9 | 1.79 | kPa |
| ∅ | 19.9 | 24.5 | 27.13 | Degree |
| δ | 13.2 | 18.4 | 19.01 | Degree |
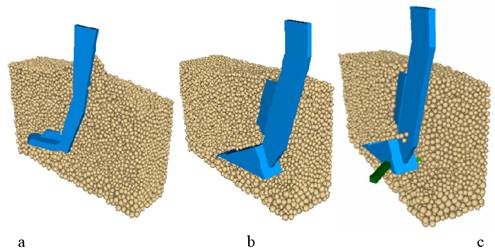
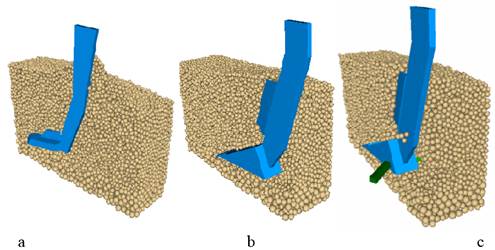
The
movement of the subsoiler, in the longitudinal section of the soil
block, shows the movement pattern of the particles during the simulation
for the three designs of subsoiler used (Figure 2).
It shows the displacement of the layers caused by the translation of
the tool. The particles are rearranged after cutting, in a position
relatively close to the initial one, and the inversion of soil layers is
not appreciated. The displacement of the particles increases in those
located in the surface layer of the soil block, which have a greater
degree of freedom.
FIGURE 2.
Section of soil de-compaction by simple (a), knife (b) and blade (c) subsoilers.
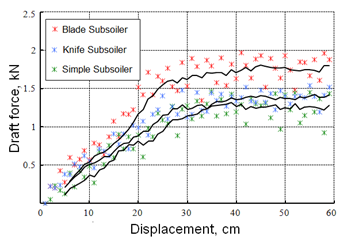
The chart of draft forces for each simulation shows a small increment on the knife subsoiler with respect to the simple one (Figure 3). The difference is probably caused by the increase in rake angle of 12º for the knife subsoiler with respect to simple one. This result is in agreement with other authors (Li et al., 2017; Ucgul et al., 2017). The blade subsoiler however, demands around 450 N more than the simple
one, suggesting that the force demanded during soil de-compaction
increases also according to the subsoiler frontal scope defined by the
width of the tool.
FIGURE 3.
Horizontal forces form simulation of simple, knife, and blades subsoilers.
However, the work performed by the blade subsoiler, with respect to the soil disturbed area, is almost two times larger compared to the simple and knife subsoilers, while the draft force only grew around 25% . For this reason the blade
subsoiler is more interesting from the energy point of view. The
magnitudes of the forces obtained from the simulation are consistent
with the results obtained by Li et al. (2016), predicted from empirical equations tillage draft for narrow tools in relation with the soil physical conditions.
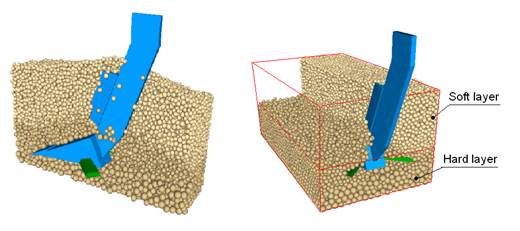
Simulation of soil hardpan disruption
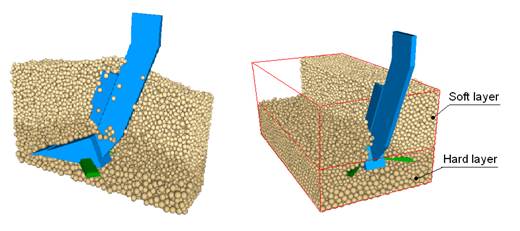
As shown in Figure 4,
the bolt subsoiler is employed in the de-compaction model of the
hardened soil layer or hardpan. To enable the analysis of the force
distribution, the calculation was divided between the resistance
demanded by the main body and the one by lateral arrows. These are the
ones that move through the hardened layer of soil and impose the
movement pattern on the particles. The results shows a vertical movement
of the soil particles during the cutting to be finally deposited
without the inversion of the soil prism.
FIGURE 4.
Soil hardpan disruption by blade subsoiler.
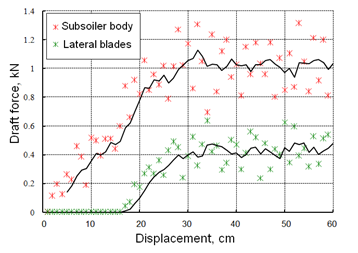
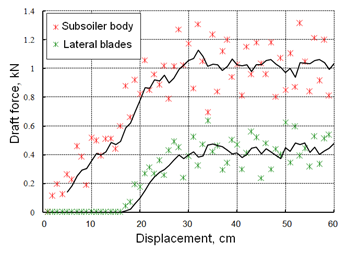
The draft force prediction from the subsoiler main body and the blades are shown in Figure 5.
A total force of 0.42 kN results from the addition of the blades to the
original subsoiler geometry. The addition of the lateral blades
increases almost three times the width of the tool, increasing the
disrupting action over the hardpan while the draft force rises only
close to 30%. Nevertheless, the soil disruption caused by the lateral
blades, should be lower than the area disrupted by the central wedge.
A
few investigations using numerical methods have been dedicated to
modelling soil-tool interaction, considering the non-homogeneous nature
of soil. Focused on that goal Mouazen and Neményi (1999),
presented a FEM model to simulate the force demanded for several
subsoilers. They concluded that more accurate draft force predictions
are obtained employing a non-homogeneous soil structure. Accordingly,
the DEM draft force results presented in Figure 5, predict with more fidelity the required forces in real soil hardpan disruption.
FIGURE 5.
Force demanded by the tool main body and lateral blades.
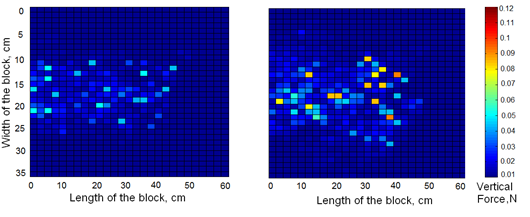
Particle force distribution
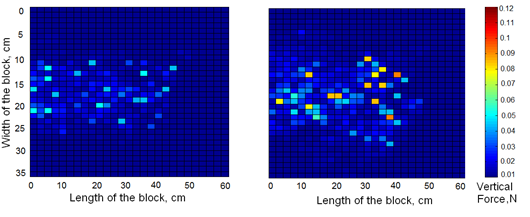
Vertical forces, calculated over soil particles placed at the tillage depth are graphically represented in Figure 6; the subsoiler was stopped at 45 cm travel in both cases. The contact surface of soil defined as soft (Fig 6a) and compacted (Fig 6b) shows the soil section susceptible to be deformed in permanent way and compacted by the tool vertical pressure.
FIGURE 6.
Vertical force on the bottom layer at soft (a), and compacted soil (b).
The results from simulations demonstrate a
rise in vertical forces associated with the level of soil density. For
the simulation in soil compacted condition, the amount of
particles submitted to pressure also increase and some maximum values
are obtained at the current tool position (Figure 6b). This result agrees with those obtained by (Zhao y Zang, 2017)
where the authors focused on the simulation of soil and tire
interaction. According to the force distribution pattern getting from
the simulation, soil condition at tillage defines the level of vertical
pressures asserted over soil at depth of tillage. Although, hardpan
resulting from repetitive tillage, the soil states becomes an important
factor in accelerating the formation of hard structure, specialty for
compacted soil.
The
simulated draft force is modified by the differences in the shape of
the subsoiler. The draft force demanded by the frontal knife remains
small compared to the simple tool, despite the bigger rake angle of the
chisel. By adding lateral blades to the subsoiler wedge, the disrupted
area is increased almost twice whereas the horizontal force increases
only 25%. On the other hand, soil hardpan disruption can be modelled
using two sections in the same virtual block of soil with different soil
strength and dry bulk density. The prediction of draft forces, measured
on the main tool body and lateral blades, independently, allows
evaluating the geometrical changes in the tool design in contrast with
the desired expansion of soil disruption. Finally, the vertical force
distribution on the layer below the tool path, in the soil virtual block
during the simulation increases for the compacted soil condition compared to the soft
soil. The intensity of the force on particles and the area under
pressure typify the loading condition by the tool shape and soil
physical state.
ARTÍCULO ORIGINAL
Simulación de la descompactación de un suelo arcilloso empleando el método de elementos discretos
Dr.C. Elvis López-Bravo [I] [*]
Dr.C. Engelbert Tijskens [II]
Dr.C. Omar González-Cueto [I]
Dr.C. Miguel Herrera-Suárez [I]
Dr.C. José Dasiell Lorenzo-Rojas [I]
[I] Universidad
Central de las Villas “Marta Abreu”, Facultad de Ciencias Agrícolas,
Departamento de Ingeniería Agrícola, Santa Clara, Villa Clara, Cuba.
[II] Catholic
University of Leuven, Faculty of Bioscience Engineering, Department of
Biosystems, Division of Mechatronics, Biostatistics and Sensors
(MeBioS), Kasteelpark Arenberg 30, B-3001 Heverlee, Belgium.
[*] Autor para correspondencia: Elvis López-Bravo, E-mail: elvislb@uclv.edu.cu
RESUMEN
La
predicción de la fuerza de tiro y la dinámica de operaciones de
descompactación de suelo fue realizada empleando el Método de los
Elementos Discretos. Los parámetros del modelo fueron definidos en
función de las propiedades mecánicas de un suelo arcilloso, previamente
obtenidos mediante ensayos de laboratorio. Las propiedades empleadas en
el modelo fueron: cohesión, adhesión, fricción interna, fricción
externa, el módulo de Young y el coeficiente de Poisson. El efecto de la
variación de la forma del subsolador fue simulado en condiciones de
suelo compacto y seco, mostrando claras variaciones en la demanda de
fuerza respecto a la geometría de la herramienta. Con el aumento en la
complejidad geométrica de la herramienta, el modelo mostró ventajas en
términos de demandada de fuerza y volumen de suelo removido. La
descompactación de un suelo con formaciones de hardpan se simuló
con el empleo de dos secciones con diferente compactación en un mismo
bloque virtual. El nivel de compactación fue obtenido mediante el empleo
de arreglos de partículas con diferente densidad. La simulación muestra
la viabilidad del modelo para determinar por separado las demandas de
fuerza en las diferentes partes del subsolador. Posibilita además
establecer el patrón de tensiones en dirección vertical sobre las
partículas en el piso de labranza.
Palabras clave:
Labranza; predicción; fricción; compactación; apero.
En
la actividad agrícola, el subsolador se emplea para el laboreo de las
capas profundas del suelo. El mismo se caracteriza por una estructura
robusta y alta demanda de energía. Fue diseñado con el fin de combatir
la compactación provocada por el paso de la maquinaria entre otros
factores. No obstante, debido a que durante la labranza no invierte el
prisma de suelo, su uso contribuye además a prevenir la erosión, la
mineralización, y la degradación del suelo en forma general (Zheng et al., 2017).
La
formación de capas endurecidas en el interior del área cultivable del
suelo, se asocia comúnmente con el arado de vertederas. Para romper
estas formaciones se necesita una operación de subsolado profundo para
restaurar la productividad del suelo, lo que posibilita la infiltración
de agua, el desarrollo radicular y la aireación del suelo. Los estudios
sobre el proceso de descompactación se han centrado en los
requerimientos en términos de fuerza de tiro, destinados a optimizar el
diseño de la herramienta. Los mismos están motivados por la necesidad de
reducir la energía consumida en relación con el diseño de la
herramienta así como la selección adecuada de los parámetros
operacionales seleccionados (Zheng et al., 2016; Li et al., 2017).
El suelo agrícola se caracteriza por no tener una densidad aparente
homogénea en las diferentes capas, algunos autores han relacionado la
densidad del mismo con su composición mineral, los factores agro físicos
circundantes y la carga sistemática adquirida como resultado de las
operaciones de transporte y labranza (Morris et al., 2010; Li et al., 2016b).
Con
el empleo del Método de los Elementos Finitos (FEM), se reportan
resultados satisfactorios en la modelación de la resistencia estructural
de la herramienta y la fuerza de tracción en condiciones estáticas.
Estos resultados han mostrado las potencialidades de los modelos FEM
para su empleo en los cálculos basados en la presión pasiva del suelo (Tadesse, 2004).
Sin embargo, este método resulta inestable para modelar flujos de
partículas y formación de grietas, lo que caracteriza las operaciones de
labranza de suelo. Por el contrario, los modelos implementados en los
Métodos de Elementos Discretos (MED) se han utilizado con éxito para
simular el flujo de material granular, basado en la interacción entre
los elementos en contacto y el efecto de las fuerzas resultantes.
Mediante el MED se describe el comportamiento dinámico y discontinuo de
las partículas del suelo y su interacción con cuerpos sólidos en
movimiento (Mak et al., 2012; López, 2014; Ding et al., 2017; Hang et al., 2017).
La
presente investigación tiene como objetivo emplear el MED para predecir
la demanda de fuerza y el comportamiento de las partículas de suelo,
mediante la simulación de operaciones de subsolado a diferentes niveles
de compactación y diferente diseño del subsolador.
Para modelar la interacción entre el suelo y la herramienta de labranza se empleó el software DEMeter++Tijskens et al. (2003), el cual se basa en el modelo de contacto clásico propuesto por Cundall (1988).
Para calcular las fuerzas de contacto entre las partículas del suelo y
el cuerpo de la herramienta se desarrolló un modelo explícito de
interacción basado en el criterio de falla del suelo de Mohr-Coulomb. El
mismo define la solución de contactos a nivel de partículas y está
compuesto por la fuerza normal, fuerza de corte, fuerza de cohesión y
fuerza de fricción. La rigidez en la dirección normal y tangencial se
calculó en función del criterio del mejor ajuste para relacionar las
propiedades elásticas del suelo con la geometría de las partículas en
contacto. Los parámetros que identifican las propiedades macroscópicas
del suelo y herramienta en el modelo fueron: módulo de Young (E), Coeficiente de Poisson (n), ángulo de friction interna (f), ángulo de fricción suelo-acero (d), cohesión del suelo (c) y adherencia (c
a
). La formulación del modelo, la calibración y la validación se
describieron en detalle en la implementación del modelo de predicción
para la labranza del suelo sin inversión (López, 2014).
Para
la simulación de las operaciones de subsolado, se emplearon dos diseños
de herramientas denominadas subsolador simple y subsolador de saetas (Figura 1). La diferencia radica en el incremento de la complejidad al agregar diferentes partes a la estructura básica. La Figura 1a
muestra la geometría del subsolador simple que posee una reja
prismática y una cuchilla dispuesta de forma vertical. El subsolador de
saetas por su parte cuenta con dos saetas de corte lateral y una
cuchilla frontal (Figura 1b). Se empleó además una modificación al subsolador de saetas denominada subsolador de cuchilla (Figura 2b).
FIGURA 1.
Subsolador Simple (a), subsolador de saetas (b).
El bloque de suelo se dimensionó a 350 mm de
ancho por 350 mm de alto con una longitud de 600 mm. Las partículas se
dividieron en tres grupos con radio promedio de 3,5, 5,0 y 7,0 mm
respectivamente, para un total de 45 000 partículas esféricas. La
densidad micro del bloque de suelo compactado se definió a la humedad de
9% para un valor de 1,3 g/cm3. Para la modelación del hardpan o capa endurecida en el suelo blando se define la humedad con un valor de 12% para una densidad aparente de 1,0 g/cm3, mientras que para la sección endurecida se establece 1.35 g/cm3.
Estas condiciones fueron seleccionadas considerando la variación en la
densidad aparente y las propiedades mecánicas utilizadas como
macro-parámetros del modelo, las cuales se muestran en la Tabla 1.
Por su parte, la distribución de la fuerza sobre las partículas de
suelo se generó a la profundidad máxima de labranza o piso de arado; la
misma se obtuvo para condiciones de suelo blando y compactado, según los
parámetros del modelo.
TABLA 1.
Parámetros macroscópicos del modelo de suelo
| Parámetros del Modelo | Condiciones del suelo |
|---|
| Suelto | Hardpan | Compactado | Unidad |
|---|
| E | 39,0 | 81,3 | 101,86 | MPa |
| v | 0,3 | 0,4 | 0,46 | |
| C | 54,5 | 104,1 | 133,60 | kPa |
| Ca | 7,6 | 1,9 | 1,79 | kPa |
| ∅ | 19,9 | 24,5 | 27,13 | Grado |
| δ | 13,2 | 18,4 | 19,01 | Grado |
Descompactación del suelo
El
movimiento del subsolador, en la sección longitudinal del interior del
bloque de suelo, muestra el patrón de movimiento de las partículas
durante la simulación para los tres diseños de subsoladores empleados (Figura 2).
En los mismos, se puede apreciar el desplazamiento de las capas
provocado por el movimiento de traslación de la herramienta, donde las
partículas se reacomodan después del corte en posiciones relativamente
cercanas a la posición inicial. En la simulación del subsolado no se
aprecia la inversión de capas de suelo. El desplazamiento de las
partículas se incrementa en las situadas en la capa superficial del
bloque de suelo, las que poseen mayor grado de libertad.
FIGURA 2.
Simulación con subsolador simple (a), de cuchilla (b) y de saeta (c).
Como se muestra en el gráfico de la demanda de fuerzas de tracción (Figura 3),
en todos los casos la fuerza se estabiliza después de un recorrido de
30 cm, lo cual coincide con la longitud de la cuña de la herramienta. La
fuerza de tracción para los tres casos, se mantiene en valores
promedios entre 1,3 y 1,8 kN, lo cual es consistente con la resistencia
que ofrece el suelo en condiciones de compactación. La diferencia mayor
entre los valores obtenidos se observa entre el subsolador simples
respecto al de saetas, con un incremento de 450 N respecto al valor
promedio. Se evidencia además, que la menor demanda la ejerce el
subsolador simple, mostrando que la demanda de tracción durante las
operaciones de subsolado se incrementa en correspondencia con el aumento
del ancho de trabajo. Estos resultados concuerdan con los obtenidos en
estudios realizados por otros autores, los cuales reportan considerable
aumento de la fuerza de tiro con el aumento del perfiles de la
herramientas de labranza (Li et al., 2017; Ucgul et al., 2017).
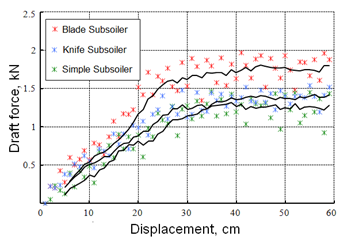
FIGURA 3.
Fuerza de tracción en los subsoladores.
No obstante a los valores de tracción
obtenidos, es de notar que la descompactación realizada por el
subsolador de saetas es al menos dos veces mayor que la removida por los
demás, mientras que el aumento en la tracción es sólo del 25%, lo que
hace la inclusión de las saetas al diseño más conveniente desde el punto
de vista energético. Las magnitudes obtenidas como resultado de la
modelación para las diferentes condiciones están en correspondencia con
los resultados obtenidos por Li et al. (2016), obtenidas mediante el empleo de ecuaciones empíricas para el cálculo de los esfuerzos en implementos de corte vertical.
Simulación del subsolado de la capa endurecida de suelo o hardpan
Como se muestra en la Figura 4, el subsolador de saetas es empleado en el modelo de descompactación de la capa endurecida de suelo o hardpan.
Para posibilitar el análisis de la distribución de las fuerzas, el
cálculo se dividió entre la resistencia que demanda el cuerpo principal y
la resistencia de las saetas laterales. Son estas las que se desplazan a
través de la capa endurecida de suelo e imponen el patrón de movimiento
a las partículas, las cuales muestran un movimiento vertical durante el
corte para ser depositas finalmente sin la inversión del prisma de
suelo.
FIGURA 4.
Modelo de subsolado de hardpan.
La predicción de la fuerza de tracción del cuerpo principal del subsolador se muestra en la Figura 5
independiente a las fuerzas obtenidas en las saetas laterales. Como
consecuencia de la adición de estas al cuerpo principal aumenta la
demanda de fuerza un promedio de 0,42 kN. Por su parte, el área de
trabajo aumenta tres veces, en tanto la fuerza de tracción solo crece en
un 30%. Esta diferencia, desde el punto de vista energético, puede
explicarse a partir de que el trabajo realizado por la cuña del
implemento es mayor debido a sus dimensiones, aumentando así la demanda
de fuerza para su desplazamiento.
No abundan en la literatura modelos donde el suelo se considere un elemento no homogéneo, como es el caso del hardpan, donde se encuentra la formación de al menos dos capas con distintas propiedades. Autores como Mouazen y Neményi (1999),
desarrollaron un modelo en elementos finitos para la simulación de la
demanda de fuerza en diferentes geometrías de implemento y concluyen que
los resultados más precisos se encontraron cuando los suelos se
consideraron con una estructura no homogénea.
FIGURA 5.
Fuerza de tracción en el cuerpo principal y las aletas del subsolador.
Distribución de tensiones en las partículas
La fuerza en sentido vertical ejercida por el subsolador sobre las partículas se muestran en la Figura 6.
En la misma se muestran los patrones de tensión en condiciones de suelo
suelto y compactado en la capa que corresponde al piso de arado. Los
resultados de la simulación muestran el aumento de la presión vertical
en el suelo asociado a la densificación del mismo. Para las condiciones
de suelo compactado se incrementan considerablemente el número de
partículas bajo presión y los valores máximos se encuentran en la zona
de contacto con el implemento (Figura 6b).
FIGURA 6.
Fuerza vertical en el piso de arado en suelo suelto (a) y en suelo compacto (b).
Estos resultados están en correspondencia con los obtenidos por Zhao y Zang (2017),
donde los autores describen la dinámica de la interacción del suelo a
diferentes densidades, así como el efecto de la geometría del
implemento. Según se muestra en el patrón de distribución de fuerzas,
las condiciones de suelo definen los valores de presión sobre el mismo a
diferentes profundidades, lo que puede alterar de forma permanente la
compactación del mismo. Sin embargo la formación del hardpan
tiene lugar por la labranza reiterada sobre la misma capa de suelo, por
lo que la intensidad de las presiones se convierte en un factor que
puede acelerar el proceso de formación de las capas endurecidas, las que
son más propensas en suelos pesados.
La
fuerza de tiro obtenida mediante la simulación, es modificada de forma
considerable con el cambio de la geometría del subsolador. Mediante la
adición de saetas de corte lateral, el ancho de trabajo se incrementó al
menos dos veces, en tanto la fuerza de tiro sólo aumentó un 25%, lo que
muestra una mejor eficiencia desde el punto de vista energético. Por
otro lado, el empleo de un bloque no homogéneo, con diferentes
densidades de suelo, posibilitó la modelación del hardpan donde
se realizó la medición independiente de las tensiones en el cuerpo y en
las saetas. Finalmente, la distribución de las fuerzas en dirección
vertical se obtuvo mediante el análisis del estado tensional del piso de
arado, donde la fuerza sobre las partículas incrementó en el suelo más
compactado así como el área de la huella de tensión del subsolador.