Rodríguez-López, Morejón-Mesa, Sosa-Guerra, Manuel-Blanco, and Martínez-Bao: Markov Model to Determinate the Rational Structure of Harvest-Transport Complex in Sugarcane

INTRODUCTION

On the influence of some agricultural and industrial aspects in the economy, it is necessary to consider the influence that the harvest-transport process has on the quality of the raw material before being processed industrially. It is evident that, although the harvest-transport process does not constitute an element that influences the production process of both cane and sugar itself, it does determine the economy of the production process. This process is developed with the use of a set of technical means, among which harvesters and means of transport (tractors and / or trucks with carts or trailers) can be mentioned and if they are irrationally organized, influence negatively the total production costs.

The introduction of more powerful and reliable machines is important to ensure that sugar industry maintains a leading role in the country's economy. Because of the rapid development of sugar industry, the improvement of equipment systems has continued, specifically in cane harvesters. In order to achieve this objective, it is essential to carry out laboratory and field investigations that enable the design of machines that provide better performance for the sugarcane harvest. The comprehensive studies of evaluations on the machines in development avoid that the errors are generalized and allow decreasing expenses and correcting possible deficiencies of design. Sugarcane harvesting machines have been subjected to various evaluations in order to increase their efficiency and comfort and reduce production costs (Fernández & Álvarez, 1988; Fernandez & Delgado, 1989; Shkiliova et al., 2000; Ortiz-Cañavate, 2003; Shkiliova, 2004; Amú, 2010).

On the rationalization of the harvest-transport process several investigations have been developed, in which different methods based on simulation and mathematical modeling have been proposed. These studies have been carried out with the purpose of determining the optimal use of different means of transport during the harvest of crops such as rice and sugarcane, as well as the determination of the rational composition of the harvest-transport brigade applying the Mass Service Theory. This theory makes it possible to analyze the productive process from the probabilistic perspective starting from the deterministic method (López et al., 2012; Matos & Iglesias, 2012; Matos et al., 2014; Matos et al., 2014; Rodríguez et al., 2015).

In the Business Unit of Base (BUB) “Héctor Molina Riaño”, Attention to Sugarcane Producers, has arisen industrial, organizational and productive problems. Therefore, the harvest-transport process may be affected by the rational composition of the harvest-transport brigade, reducing the stability of the flow of the technological process and increasing its costs.

For this reason, it is necessary to investigate the rational composition of the harvest-transport complex of sugarcane in the BUB “Héctor Molina Riaño”, with the purpose of achieving greater stability and obtaining economic advantages in it. For the above mentioned the investigation had as objective to determine the rational structure of the complex harvest-transport of sugarcane through the model of Markov.

MATERIALS AND METHODS

The experimental research program was developed in the BUB "Héctor Molina Riaño", Mayabeque, Cuba; during the agro technical period of the sugarcane harvest in 2017, carrying out the fieldwork and the characterization of the experimental area. Technological and operation evaluations were carried out on two (2) CASE IH AUSTOFT A 8800 harvesters and the mechanized media involved in transport. These means are made up of Belarus 1523 tractors with VTX 10000 self-tilting trailers of 10 t capacity and hauling trucks HOWO SINOTRUK with two (2) trailers of 60 t capacity in total (20 t each).

Markov Model for Rationalization of the Harvest - Transport Brigade

For the analysis of the rational structure of the harvest-transport complex of sugarcane using Markov Model, it is assumed that it is a stochastic process, since it varies exponentially in time. It is a succession of observations whose values cannot be accurately predicted (Kijima, 1997, 2013, Hermanns, 2002a, 2002b; Bini et al., 2005; Ibe, 2013). For this model, the states considered are sugarcane in harvesting Ec, sugarcane in transportation Et and sugarcane in reception center Er. The amount of transportation means necessary is obtained by the deterministic method and it is combined with the transition probability criteria from the elaborated matrix (Conlisk, 1976; Tijms & Tijms, 1994; Bolch et al., 2006; Ching & Ng, 2006; Sánchez, 2016).

To establish the probability of transition in each state of the ones declared, authors start from the photo chronometry of each process according to Aguilera and Fonseca (2013) and Rodríguez et al. (2015), determining the coefficients of technical availability of the harvesters and means of transport, as it is shown in expression 1.

K d = T o / (T o + T J)

(1)

where:

- total time (useful work) of operation under design conditions, h;

- total time of stop due to technical problems, h.

In order to form the transition matrix, the probability of transition or non-transition from one state to another must be determined through Poisson table, according to Yesin & Sevostyanov (2014). For this, authors considered the observations made to the line of trucks in the mill and the mathematical hope for the harvest λc and the transport λt (expression 2 and 3) is determined.

For the harvest, it is determined from its coefficient of technical availability:

λ_{c} = n_{c} * k_{d_{c}}

(2)

where:

n_c

- number of harvesters;

For transport, its technical availability is taken into account:

λ_{t} = n_{t} * k_{d t}

(3)

where:

n_t

- number of trucks;

Having λc, λt, and K (number of trucks to observe) for the combine and transport, the probabilities of transition can be determined through the Poisson tables.

To determine the probability of transition (Pt) and not transition (Pnt) of the plant, 15 observations were made that were averaged, determining the number of trucks waiting to deliver the product (ncer) and the total number of trucks in the reception center (ntr);

P_{nt} \equiv \frac{n_{cer}}{n_{tr}}

(4)

Taking into account the probabilities of non-transition, the transition probabilities can be obtained:

P_{t =} 1 - P_{n t}

(5)

By means of the above, the transition matrix can be determined from one state to another:

\begin{matrix} E_{c} \\ E_{t} \\ E_{r} \end{matrix} \begin{matrix} \begin{matrix} E_{c} & E_{t} & E_{r} \end{matrix} \\ (\begin{matrix} P_{nt} & P_{t} & 0 \\ 0 & P_{nt} & P_{t} \\ P_{t} & 0 & P_{nt} \end{matrix}) \end{matrix}

(6)

Based on the analysis previously carried out, an estimation of the economic impact due to the rupture of the Cpet cycle can be obtained from the determination of the costs for stops in each element of the cycle and the probability of not transiting from one state to another.

C_{pet=} (C_{pc} {*P}_{ntc}) + (C_{pt} {*P}_{{nt}_{t}}) + (C_{pcr} {*P}_{{nt}_{r}});peso/h

(7)

where:

Cpc, pt and Pcr

- cost per stop in the harvest, transport and mill reception center respectively; peso / h

With the direct costs of operation, the costs per stop of the combine and transport can be determined:

C_{PC} \equiv C_{exp} \equiv C_{dc} {+C}_{c} {+C}_{l} {+C}_{mr} {+C}_{soc}, peso / h

(8)

where:

Cexp

- operation costs, peso / h;

Cdc

-Cost of depreciation of the harvester, peso / h;

- Cost of fuel consumed, peso / h;

- Cost of the lubricant consumed, peso / h;

Cmr

-Cost of maintenance and repair operations, peso / h;

Csoc

-Cost in the combine operator's salary, peso / h.

Similarly, the cost of the stopping time of the means of transportation can be determined, using expression 9:

C_{PT} = \cdot C_{dt} + C_{mr} + C_{sot}, p e s o / h

(9)

where:

Cdt

- Cost of depreciation of the means of transport, peso / h;

Cmr

-Cost of maintenance and repair operations, peso / h;

Csot

- Cost in salary of the operator of the means of transport, peso / h.

Regarding the costs for stops at the reception center, the salary of the workers linked to the process, the fuels and lubricants consumed in the process, as well as the costs for maintenance and electricity consumed are taken into account as it is shown in expression 9,.

C_{pcr} \equiv C_{s} {±C}_{c} {±C}_{mr} {±C}_{e}, peso / h

(10)

where:

-cost for electricity consumption, peso / h

ANALYSIS OF THE RESULTS

Analysis of the Rational Structure of the Harvest-Transport Complex of Sugarcane using Markov Model

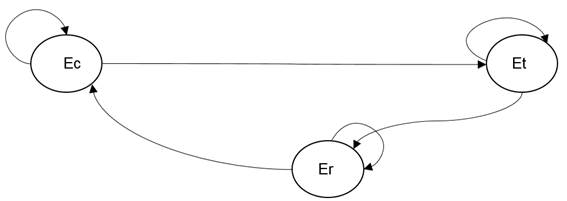
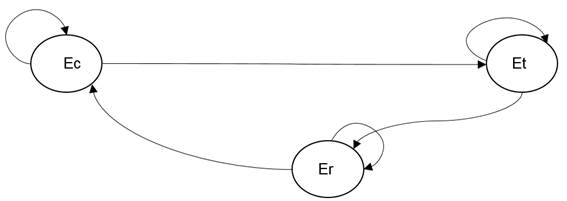
For the realization of the rational composition of the harvest-transport-reception complex of sugarcane using the Markov Model, three (3) states were defined, which were the cane in harvesting Ec, the cane in transportation Et and the cane in reception Er , represented in figure 1 and where the flow of these states is shown.

FIGURE 1

Diagram of transition of states in the harvest-transport and reception of sugarcane.

For the application of this model, lambda values (λ) were determined, which are shown in Table 1, taking into account the technical unavailability of the harvester (1-Kd) and the means of transport (trucks) which were 0.13 and 0.05, respectively. It was also taken into account that there were two (2) harvesters in the sugarcane harvest state, and 2.25 trucks were needed to transport cane, according to the deterministic method, so that there is a cycle in the process harvest-transport-reception. For the state of cane in reception, given the observations made, a transition probability of 0.41 and a non-transition of 0.59 were obtained.

TABLE 1

Data needed to prepare the transition matrix

State	Kd	1-Kd	λ	k
Ec	0,87	0,13	1.7	2
Et	0,95	0,05	2,9	3

By means of the results obtained, the transition matrix could be formed. In the harvesting state, the transition probability was 0.87 and the non-transition probability was 0.13. Non-transition probability for transport cane was 0.05 and 0.95 for transition. For reception, 0.41 for transition and 0.59 for non-transition as shown in matrix 10.

\begin{matrix} E_{c} \\ E_{t} \\ E_{r} \end{matrix} \begin{matrix} \begin{matrix} E_{c} & E_{t} & E_{r} \end{matrix} \\ (\begin{matrix} 0,13 & 0,87 & 0 \\ 0 & 0 .05 & 0 .95 \\ 0 .41 & 0 & 0 .59 \end{matrix}) \end{matrix}

(10)

While analyzing the previous results, and determining the probabilities through the Poisson tables, as shown in Table 2, it is obtained that the probability of non-failure or breakage of none of the harvesters is 82%. The probability of a failure in at least one (1) is 16.37%, which makes it possible to foresee the effects it will have on the cycle due to the stoppage of a harvester. When analyzing the case of trucks, it is obtained that the probability of failure or breaks of any truck is 95.12%, and that there is a failure in at least one (1) of 4.76% decreasing to 0.12% of breaking two (2) at the same time.

TABLE 2

Ratio of probability of harvester and truck breakages

Type	Number	Probability of a technical failure
Harvester	0	0,8187
	1	0,1637
	2	0,0164
Trucks	0	0,9512
	1	0,0476
	2	0,0012
	3	0,0000

As mentioned above, the deterministic method showed that 2.25 trucks are needed for the existence of a cycle in the process. Therefore, taking into account the low probability of breakage of at least one harvester and / or truck, it can be assumed that the brigade, for the agricultural yield of 22.8 t / ha will be made up of two (2) harvesters with two (2) moving tractors and two (2) trucks for the transfer to the plant. Since the filling time is 2.66 h and the cycle time of 4.94 h, the probability that the harvester waits for external means of transports is almost null.

Results of the Costs for Cycle Stops

From the transition matrix, the cost can be determined if the transportation cycle is stopped in the states declared (Ec, Et and Er) of the process, obtaining a cost of 10.73 pesos / h, when the sum of stop costs in the states considering the probability of non-transition amounts to 5.29; 0.82 and 4.62 pesos / h, respectively. However, as the probability of non-transition was not taken into account, a cost per plant stop of 7.84 pesos / h, a cost per harvest stop of 45, 47 peso / h and transport stop of 16.56 peso / h were obtained.

TABLE 3

List of expenses for stops and the probability of non-transition

	C_p, peso/h	P_nt	Cp_es, peso/h
E_c	45,57	0,13	5,92
E_t	16,56	0,05	0,82
E_r	7,84	0,59	4,62
Ciclo
Cp_est peso/h		10,73

CONCLUSIONS

Markov Model showed that for a field with a yield of 22.8 t / ha the brigade will consist of two (2) harvesters and (2) two means of transport, since the probability that the harvester waits for means of external transport is almost null, being the expense per cycle stop (harvest-transport-reception) of 10.73 peso / h.
Markov Model allows defining the rational conformation of the harvest-transport-reception brigade from another model or method that proposes possible compositions.

REFERENCES

AGUILERA, O.; FONSECA, J.: Aplicación de un procedimiento para evaluar la eficiencia en el proceso de explotación según el consumo de combustible de las cosechadoras de caña KTP-2M, Ed. Grin Verlag, Berlín, Germany, 2013, ISBN: 10: 365646779X; ISBN-13: 978-3656467793.

AMÚ, L.G.: “Logística de cosecha. Evaluación de tiempos y movimientos. Indicadores y control”, Revista Tecnicaña, 26: 25-30, 2010, ISSN: 0123-0409.

BINI, A.D.; LATOUCHE, G.; MEINI, B.: Numerical methods for structured Markov chains, Ed. Oxford University Press on Demand, New York, USA, 2005, ISBN: 0-19-852768-3.

BOLCH, G.; GREINER, S.; DE MEER, H.; TRIVEDI, K.S.: Queueing networks and Markov chains: modeling and performance evaluation with computer science applications, Ed. John Wiley & Sons, 2006, ISBN: 0-471-79156-3.

CHING, W.K.; NG, M.K.: Markov Chains: Models, Algorithms and Applications, Ed. Springer US, New York, USA, 2006, ISBN: 978-1-4614-6312-2.

CONLISK, J.: “Interactive markov chains”, Journal of Mathematical Sociology, 4(2): 157-185, 1976, ISSN: 0022-250X.

FERNÁNDEZ, P.A.; ÁLVAREZ, R.E.: “Determinacion de los principales indicadores de fiabilidad de la cosechadora de cana KTP-1.”, Revista Ciencias Técnicas Agropecuarias, 1(3): 57-60, 1988, ISSN: 1010-2760, E-ISSN: 2071-0054.

FERNANDEZ, P.A.; DELGADO, O.N.: “Analisis del trabajo del parque de tractores en funcion del numero de roturas imprevistas.”, Revista Ciencias Técnicas Agropecuarias , 2(1): 27-32, 1989, ISSN: 1010-2760, E-ISSN: 2071-0054.

HERMANNS, H.: “Interactive markov chains”, En: Interactive Markov Chains, Ed. Springer, pp. 57-88, 2002a.

HERMANNS, H.: “Interactive Markov chains in practice”, En: Interactive Markov Chains, Ed. Springer-Verlag Berlin Heidelberg, vol. 2428, Berlin, Germany, pp. 125-146, 2002b, ISBN: 978-3-540-45804-3.

IBE, O.: Markov processes for stochastic modeling, Ed. Newnes, 2013, ISBN: 0-12-407839-7.

KIJIMA, M.: Markov Processes for Stochastic Modeling, Ed. Chapman & Hall, 1st edición ed., Cambridge, USA, 194 p., 1997, ISBN: 0412606607.

KIJIMA, M.: Markov processes for stochastic modeling, Ed. Springer, Cambridge, USA, 2013, ISBN: 1-4899-3132-5.

LÓPEZ, Y.M.; RAMÍREZ, N.M.; DE ARMAS, R.L.P.; MACHADO, Y.M.: “Optimización del proceso Cosecha-Transporte-Recepción de la caña de azúcar”, Revista Cubana de Ciencias Informáticas, 5(3), 2012, ISSN: 2227-1899.

MATOS RAMÍREZ, N.; IGLESIAS CORONEL, C.; GARCÍA CISNEROS, E.: “Organización racional del complejo de máquinas en la cosecha-transporte-recepción de la caña de azúcar en la Empresa Azucarera ARGENTINA”, Revista Ciencias Técnicas Agropecuarias , 23(2): 27-33, 2014, ISSN: 2071-0054.

MATOS, R.N.; IGLESIAS, C. E.: “Modelo económico-matemático para la organización racional de los medios técnicos en la cosecha-transporte-recepción de la caña de azúcar”, Revista de Ciencias Técnicas Agropecuarias, 21(3): 49-54, 2012, ISSN: 1010-2760, E-ISSN: 2071-0054.

MATOS, R.N.; IGLESIAS, C.E.; GARCÍA, C.E.: “Organización racional del complejo de máquinas en la cosecha - transporte - recepción de la caña de azúcar en la Empresa Azucarera “Argentina””, Revista Ciencias Técnicas Agropecuarias , 23(2): 28-33, 2014, ISSN: 1010-2760, E-ISSN: 2071-0054.

ORTIZ-CAÑAVATE, J.: Las máquinas agrícolas y su aplicación, Ed. Mundi Prensa, reimpresa ed., Madrid, España, 526 p., 2003, ISBN: 84-8476-117-7.

RODRÍGUEZ, L.Y.; MOREJÓN, M.Y.; SOSA, G.D.; MARTÍNEZ, B.O.: “Modelación matemática del complejo cosecha-transporte de la caña de azúcar para su racionalización”, Revista de Ciencias Técnicas Agropecuarias , 24(Exp.): 42-48, 2015, ISSN: 1010-2760, E-ISSN: 2071-0054.

SÁNCHEZ, B.A.: “Aplicación de Cadenas de Markov en un proceso de producción de plantas in vitro”, Tecnología en Marcha, 29(1): 74-82, 2016, ISSN: 2215-3241.

SHKILIOVA, L.: “Fundamento teorico para determinar la efectividad de mantenimiento técnico”, Revista Ciencias Técnicas Agropecuarias , 13(1): 51-53, 2004, ISSN: 1010-2760, E-ISSN: 2071-0054.

SHKILIOVA, L.; SUÁREZ, P.C.; IGLESIAS, C.C.: “Fiabilidad de los complejos tecnológicos”, Revista Ciencias Técnicas Agropecuarias , 9(3-4): 23-29, 2000, ISSN: 1010-2760, E-ISSN: 2071-0054.

TIJMS, H.C.; TIJMS, H.C.: Stochastic models: an algorithmic approach, Ed. John Wiley & Sons Chichester, vol. 994, 1994.

YESIN, K.S.; SEVOSTYANOV, A.L.: “Logistics of Grain Transportation: Program Exploitation for Calculation of Optimum Number of Vehicles.”, Ecology and Transport, Bulletin of PNU, 32(1), 2014, ISSN: 1996-3440, Disponible en:Disponible en:http://pnu.edu.ru/media/vestnik/articles-2014/117-124 , [Consulta: 10 de diciembre de 2017].

INTRODUCCIÓN

Sobre la influencia de algunos aspectos agrícolas e industriales en la economía, es necesario considerar la influencia que tiene el proceso de cosecha-transporte en la calidad de la materia prima antes de ser procesada industrialmente; evidenciándose que aunque el proceso cosecha-transporte no constituye un elemento que influye en el proceso de producción tanto de la caña, como de azúcar en sí, si determina la economía del proceso productivo, pues este proceso se desarrolla con el empleo de un conjunto de medios técnicos entre los que se pueden citar las cosechadoras y los medios de transporte (tractores y/o camiones con carretas o remolques), los cuales, sino son racionalmente organizados influyen negativamente en los costos totales de producción.

La introducción de máquinas más potentes y fiables, son pasos importantes para lograr que la industria azucarera mantenga un papel protagónico en la economía del país. Como consecuencia del vertiginoso desarrollo de la industria azucarera, se ha continuado el perfeccionamiento de los sistemas de equipos, específicamente en las cosechadoras de caña. Para lograr este objetivo se hace indispensable realizar investigaciones de laboratorio y de campo que permitan concebir máquinas que proporcionen mejores prestaciones para la cosecha de caña de azúcar. Los estudios integrales de evaluaciones sobre las máquinas en desarrollo evitan que los errores se generalicen, así como la disminución de los gastos y la corrección de posibles deficiencias de diseño. Las máquinas cosechadoras de caña de azúcar han sido sometidas a diversas evaluaciones con vistas a elevar su eficiencia, confort y reducir los costos de producción (Fernández y Álvarez, 1988; Fernandez y Delgado, 1989; Shkiliova et al., 2000; Ortiz-Cañavate, 2003; Shkiliova, 2004; Amú, 2010).

Sobre la racionalización del proceso cosecha-transporte se han desarrollado varias investigaciones, en las que se han planteado diferentes métodos basados en la simulación y la modelación matemática, estos estudios se han realizado con el propósito de determinar el uso óptimo de los diferentes medios de transporte durante la cosecha de cultivos como el arroz y la caña de azúcar, así como la determinación de la composición racional de la brigada cosecha-transporte aplicando la Teoría del Servicio Masivo. Esta teoría posibilita analizar el proceso productivo desde la perspectiva probabilística partiendo del método determinista (López et al., 2012; Matos y Iglesias, 2012; Matos et al., 2014; Matos et al., 2014; Rodríguez et al., 2015).

En la UEB Atención a Productores Cañeros “Héctor Molina Riaño” han surgido problemas industriales, organizativos y productivos. Por lo que el proceso cosecha- transporte puede estar afectado por la composición racional de la brigada cosecha- transporte, disminuyendo la estabilidad del flujo del proceso tecnológico y sus costos.

Por tal razón surge la necesidad de investigar la composición racional del complejo cosecha-transporte de la caña de azúcar en la Unidad Empresarial de Base (UEB) “Héctor Molina Riaño”, con el propósito de lograr una mayor estabilidad y obtener ventajas económicas en el mismo. Por lo anterior planteado la presente investigación tiene como objetivo, determinar la estructura racional del complejo cosecha-transporte de la caña de azúcar a través del modelo de Markov.

MÉTODOS

El programa de las investigaciones experimentales se desarrolló en la UEB “Héctor Molina Riaño”, Mayabeque, Cuba; durante el período agrotécnico de la cosecha de la caña de azúcar, en la zafra correspondiente al 2017, realizándose el trabajo de campo y la caracterización del área experimental. La evaluación tecnológica y de explotación se le realizó a dos cosechadoras CASE IH AUSTOFT A 8800 y a los medios mecanizados que intervienen en el transporte, estos medios están conformados por tractores Belarus 1523 con remolques autobasculantes VTX 10000 de capacidad 10 t y por camiones de tiro HOWO SINOTRUK con dos remolques de capacidad 60 t en total (20 t cada uno), la distancia media total de tiro de 18 km, de ellos 12 km por viales de terraplén y el resto de viales asfaltados, de categorías III y II respectivamente.

Modelo de Markov para racionalización de la brigada cosecha - transporte

Para el análisis de la estructura racional del complejo cosecha-transporte de la caña de azúcar empleando el modelo de Markov, se parte de que es un proceso estocástico, pues varía en el tiempo de forma exponencial, lo cual no es más que una sucesión de observaciones y los valores de estas no se pueden predecir exactamente (Kijima, 1997, 2013, Hermanns, 2002a, 2002b; Bini et al., 2005; Ibe, 2013). Para dicho modelo se tiene en cuenta que los estados que forman el proceso son: caña de azúcar en cosecha E_c, caña de azúcar en transporte E_t y caña de azúcar en el centro de recepción E_r y la cantidad de medios de transporte necesarios se obtiene por el método determinista y se combina con los criterios de probabilidad de transición provenientes de la matriz elaborada (Conlisk, 1976; Tijms y Tijms, 1994; Bolch et al., 2006; Ching y Ng, 2006; Sánchez, 2016).

Para establecer la probabilidad de transición en cada estado de los declarados se parte del fotocronometraje de cada proceso según Aguilera y Fonseca (2013) y Rodríguez et al. (2015), determinándose los coeficientes de disponibilidad técnica de las cosechadoras y los medios de transporte, como se muestra en la expresión 1.

Kd = \frac{To}{To + TJ}

(1)

donde:

T₀

- tiempo total (trabajo útil) de operación en condiciones de diseño, h;

T_J

-tiempo total de parada por problemas técnicos, h.

Con el objetivo de formar la matriz de transición se debe determinar la probabilidad de transición o no transición de un estado a otro a través de las tabla de Poisson según Yesin y Sevostyanov (2014), para esto se tienen las observaciones realizadas a la cola de los camiones en el central y se determina la esperanza matemática para la cosecha $λ$ _c y el transporte $λ$ _t (expresión 2 y 3).

Para la cosecha se determina a partir del coeficiente de disponibilidad técnica de la misma:

λ_{c} = n_{c} * k_{d_{c}}

(2)

donde:

$n_{c}$ - número de cosechadoras;

Para el transporte se tiene en cuenta además de la disponibilidad técnica de los mismos:

λ_{t} = n_{t} * k_{d t}

(3)

donde:

$n_{t}$ - número de camiones.

Teniendo $λ$ _c, $λ$ _t, y K (número de camiones a observar) para la cosechadora y el transporte se pueden determinar las probabilidades de transición a través de las tablas de Poisson.

Para determinar la probabilidad de transición (P_t) y no transición (P_nt) del central se hicieron 15 observaciones que se promediaron determinando el número de camiones en espera para entregar el producto (n_cer) y el total de camiones en el centro de recepción (n_tr);

P_{nt} \equiv \frac{n_{cer}}{n_{tr}}

(4)

Teniendo en cuenta las probabilidades de no transición se puede obtener las probabilidades de transición:

P_{t =} 1 - P_{n t}

(5)

Mediante lo antes expuesto se puede determinar la matriz de transición de un estado a otro:

\begin{matrix} E_{c} \\ E_{t} \\ E_{r} \end{matrix} \begin{matrix} \begin{matrix} E_{c} & E_{t} & E_{r} \end{matrix} \\ (\begin{matrix} P_{nt} & P_{t} & 0 \\ 0 & P_{nt} & P_{t} \\ P_{t} & 0 & P_{nt} \end{matrix}) \end{matrix}

(6)

Basado en el análisis anteriormente realizado se puede obtener una estimación de la afectación económica por la rotura del ciclo C_pet a parir de la determinación de los costos por paradas en cada elemento del ciclo y la probabilidad de que no se transite de un estado a otro del mismo.

C_{pet=} (C_{pc} {*P}_{ntc}) + (C_{pt} {*P}_{{nt}_{t}}) + (C_{pcr} {*P}_{{nt}_{r}});peso/h

(7)

donde:

C_pc, C_{pt y} C_pcr

- costo por parada en la cosecha, transporte y centro del recepción del central respectivamente; peso/h

Con los Costos directos de explotación se pueden determinar los costos por parada de la cosechadora y del transporte:

C_{PC} {=C}_{exp} {=C}_{dc} {+C}_{c} {+C}_{l} {+C}_{mr} {+C}_{soc}, peso / h

(8)

donde:

C_exp

-Costos de explotación, peso/h;

C_dc

-Costo de depreciación de la cosechadora, peso/h;

C_c

-Costo del combustible consumido, peso/h;

C_l

-Costo del lubricante consumido, peso/h;

C_mr

-Costo de las operaciones de mantenimiento y reparación, peso/h;

C_soc

-Costo en salario del operador de la cosechadora, peso/h.

De igual forma se puede determinar el costo del tiempo de parada de los medios de transporte, empleándose la expresión 9:

C_{PT} = \cdot C_{dt} + C_{mr} + C_{sot}, p e s o / h

(9)

donde:

C_dt

- Costo de depreciación del medio de transporte, peso/h;

C_mr

-Costo de las operaciones de mantenimiento y reparación, peso/h;

C_sot

-Costo en salario del operador del medio de transporte, peso/h.

En cuanto a los costos por paradas en el centro de recepción se tienen en cuenta el salario de los trabajadores vinculados al proceso, los combustibles y lubricantes consumidos en el proceso así como los mantenimientos y la electricidad consumida como se muestra en la expresión 9

C_{pcr} \equiv C_{s} {±C}_{c} {±C}_{mr} {±C}_{e}, peso / h

(10)

donde:

-Costo por consumo de energía eléctrica, peso/h

ANÁLISIS DE LOS RESULTADOS

Análisis de la estructura racional del complejo cosecha-transporte de la caña de azúcar empleando el modelo de Markov

Para la realización de la composición racional del complejo cosecha-transporte-recepción de la caña de azúcar empleando el modelo de Markov se definieron tres estados que fueron la caña en cosecha E_c, la caña en transporte E_t y la caña en recepción E_r, representándose en la Figura 1 y donde se muestra el flujo de estos estados.

FIGURA 1

Diagrama de transición de estados en la cosecha-transporte y recepción de la caña de azúcar.

Para la aplicación de este modelo se determinaron valores de landa (λ) que se muestran en la Tabla 1, para esto se tuvo en cuenta la no disponibilidad técnica de la cosechadora (1-K_d) y los medios de transporte (camiones) siendo de 0,13 y 0,05 respectivamente, también se tuvo en cuenta que en el estado caña en cosecha existían dos cosechadoras y para caña en transporte según el método determinista se necesitan 2,25 camiones para que exista un ciclo en el proceso cosecha-transporte-recepción. Para el estado de caña en recepción por las observaciones realizadas se obtuvo una probabilidad de transición de 0,41 y de no transición de 0,59.

TABLA 1

Datos necesarios para elaborar la matriz de transición

Estado	K_d	1-K_d	λ	k
E_c	0,87	0,13	1,7	2
E_t	0,95	0,05	2,9	3

Mediante los resultados obtenidos se puede formar la matriz de transición donde en el estado en cosecha la, probabilidad de transición es de 0,87 y la de no transición es de 0,13, siendo para caña en transporte de 0,05 la de no transición y 0,95 la de transición y para la recepción 0,41 la de transición y 0,59 la de no transición como se muestra en la matriz 10.

\begin{matrix} E_{c} \\ E_{t} \\ E_{r} \end{matrix} \begin{matrix} \begin{matrix} E_{c} & E_{t} & E_{r} \end{matrix} \\ (\begin{matrix} 0,13 & 0,87 & 0 \\ 0 & 0,05 & 0,95 \\ 0,41 & 0 & 0,59 \end{matrix}) \end{matrix}

(10)

Al analizar los resultados anteriores y determinar las probabilidades a través de las tablas de Poisson, como se muestra en la Tabla 2 se obtiene que la probabilidad de que no presenten fallas o roturas ninguna de las cosechadoras es del 82% y de que se produzca una falla en al menos una es del 16,37% lo que permite prever la afectación que va a haber en el ciclo por la parada de una cosechadora. Al analizar el caso de los camiones, se obtiene que la probabilidad de que no presenten fallas o roturas ningún camión es del 95,12%, y de que se produzca una falla en al menos uno del 4,76% disminuyendo a 0,12% de que se rompan dos al mismo tiempo.

TABLA 2

Relación de probabilidad de roturas de cosechadoras y camiones

Tipo	Cantidad de medios	Probabilidad de que ocurra una falla técnica
Cosechadora	0	0,8187
	1	0,1637
	2	0,0164
Camiones	0	0,9512
	1	0,0476
	2	0,0012
	3	0,0000

Como se menciona anteriormente el método determinista arrojó que se necesitan 2,25 camiones para que exista un ciclo en el proceso, por tanto, teniendo en cuenta la baja probabilidad de roturas de al menos una cosechadora y/o camión se puede tomar como que la brigada, para el rendimiento agrícola de 22,8 t/ha quedará conformado por dos cosechadoras con igual número de tractores movedores y dos camiones para el traslado al central, pues siendo el tiempo de llenado de 2,66 h y el tiempo de ciclo de 4,94 h la probabilidad de que la cosechadora espere por medios de transportes externos es casi nula.

Resultados de los costos por paradas del ciclo

A partir de la matriz de transición se puede tener una estimación del costo si se detiene el ciclo de transportación, en los estados declarados (E_c, E_t y E_r) del proceso (Tabla 3), obteniéndose un costo de 10,73 peso/h, al efectuarse la suma de los gastos por parada en los estados considerando la probabilidad de no transición asciende a 5,29; 0,82 y 4,62 peso/h, respectivamente, sin embargo, al no considerarse la probabilidad de no transición se obtuvo un costo por parada del central de 7,84 peso/h, un costo por parada de la cosecha de 45,47 peso/h y por parada del transporte de 16,56 peso/h.

TABLA 3

Relación de gastos por paradas y la probabilidad de no transición

	C_p, peso/h	P_nt	Cp_es, peso/h
E_c	45,57	0,13	5,92
E_t	16,56	0,05	0,82
E_r	7,84	0,59	4,62
Ciclo
Cp_est peso/h		10,73

CONCLUSIONES

Mediante el modelo de Markov se obtuvo que para un campo con un rendimiento 22,8 t/ha la brigada quedará conformada por dos cosechadoras y dos medios de transporte ya que la probabilidad de que la cosechadora espere por medios de transportes externos es casi nula, siendo el gasto por parada del ciclo (cosecha-transporte-recepción) de 10,73 peso/h.
El modelo de Markov permite definir la conformación racional de la brigada cosecha-transporte- recepción a partir de otro modelo o método que proponga posibles composiciones.

Markov Model to Determinate the Rational Structure of Harvest-Transport Complex in Sugarcane

REFERENCES

Modelo de Markov para determinar la estructura racional del complejo cosecha-transporte en caña de azúcar