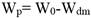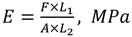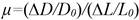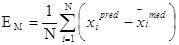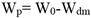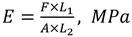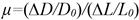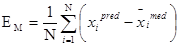Translate PaperORIGINAL ARTICLE http://opn.to/a/qjuzF
http://opn.to/a/qjuzFMathematical Techniques to Infer Post-Harvest Changes in the Properties of Agricultural Products
[
*
] Correspondence to author: Lazara Rangel-Montes de Oca. e-mail: lazarar@unah.edu.cu
ABSTRACTUsing statistical-mathematical methods, changes in the properties of agricultural products are inferred, in this case pineapple (Annanas Comosus) and Guava stored at room temperature, according to the CODEX and FAO standards. The use of statistical-mathematical modeling utilized for pineapple allowed establishing the maximum storage period of this fruit, defining dates of commercialization as fresh fruit and determining the speed with which changes in their properties occur. The mechanical response of guava (Red Dwarf variety EEA 1-23) to static charges using the Finite Element Method (MEF) was also simulated, obtaining a model capable of predicting the behavior of the fruit with an approximation of 90%. That made possible to perform virtual tests of guavas under load conditions in which physical tests are difficult to apply.
INTRODUCTIONCarrying out the appropriate conservation in the post-harvest stage of the products is among the main steps aimed at achieving food sovereignty and improving the efficiency in the use of agricultural products, which is only possible if a quality product is available with a high degree of acceptance (Hernández et al., 2005; García, et al., 2010; Mogollón et al., 2011; Fernández et al., 2012; Ramos et al., 2013; Jímenez, 2015; López, 2017).The quality of agricultural products refers to a series of attributes fundamentally related to their general health and commercial life. The knowledge of their main physical-mechanical and organoleptic properties using traditional methods and, more recently, the non-destructive ones, plays an indispensable role for a good presentation and conservation of them, which allows defining the most appropriate management during the periods of pre-harvest, harvest and post-harvest (Schofield y Wroth, 1968; Yirat Becerra et al., 2009; Mogollón et al., 2011; Jiménez, 2015; López, 2017). The non-destructive methods have the possibility of being used for the automation of online selection processes and in the development of scientific research since it is possible to homogenize the criterion of selection of samples for studies where several qualities of the fruit intervene and that, historically, were carried out using the criteria of experts. (FAO, 2018). In recent years, as a result of the development of electronics and computers, considerable progress has been made in the use of these applications for teaching and research purposes. That is demonstrated in the proposal in which studies of quality applied to fruits are repeated from new forms and methods derived from the technological development, such as those related to modeling and simulation of fruits or processes that occur essentially during the post-harvest stage. It facilitates making measurements less cumbersome and more precise, also enabling the non-destructive monitoring of this important attribute for fresh fruits, during storage at room temperature (Park,B., et..al., 2001., Garcia ,2007).
On the other hand, the use of Finite Element Method (FEM) for the simulation of mechanical response to static charges (Silvestre, 1998., Lu et al, 2006., Jamal et al, 2005., Kabas, et al, 2008), that is a tool for performing non-destructive tests on fruits, allows predicting optimum storage and handling conditions during transportation in order to improve harvest and post-harvest processes to maintain their quality. During last three decades, the method has been successfully applied in Cuba in the field of agricultural engineering, fundamentally in modeling soil-agricultural implement interaction (Herrera et al., 2008; Martínez et al., 2011; López, 2017). The study aims to characterize from the use of mathematical tools, the post-harvest behavior of the main physical, chemical and mechanical properties linked to the quality of agricultural products.
MATERIALS AND METHODSThrough the Mexican Standard (NMX-FF-041-SCFI-2002) the selection of guava fruits (red dwarf) and pineapple (cayena lisa.) was carried out. A total of 110 fruits was sampled (40 guavas and 70 pineapples), 10 fruits were removed daily, during the experimental days and, for guava, they were divided into two groups by states of maturation (only two states being chosen because the fruit is usually collected for export in state I, that is green) and is usually more susceptible to damage in state III (mature). Due to that they are the most interesting and consist of 20 fruits each. Those 20 fruits of each state are divided into groups of 10, one group to determine mass, density and firmness at compression to 3% of the polar diameter (Ф), and a group of 10 for the determination of the elasticity limit, Young's modulus and Poisson's coefficient.
The size is obtained by polar and equatorial diameter with the use of a caliper from 0 to 150 mm ± 0.05 mm. The mass is determined with an electronic balance model LG-1001ª / 0.1 (g), making three repetitions per fruit and determining the weight losses by Equation 1. The IC was determined by the method of capturing images, photographing the fruits with a digital camera model CANON PowerShot A630 8.5 mega-pixels, then exported to the portable software ADOBE PHOTOSHOP v.10, obtaining the numerical representation of the variables L * a * and b *, which establishes coordinates in a color plane that creates the maturation scale by its coordinates (García et al., 2010).
Where:- weight of fruit on day zero, g
- weight of fruit on day of interest, g
The contents of soluble solids (SSC, for its acronym in English) are evaluated and density is determined through the principle of Archimedes.
Resistance to penetration (firmness): It was obtained from the puncture test for the case of pineapple and compression to 3% of the polar diameter in the case of the guava, with the digital durometer, Model CEMA-C08, 0 to 1000 (kgf / cm2) / 0.01 (kgf / cm2), of national manufacturing, according to the Magness-Taylor principle in three equidistant points, separated at approximately 120º of others (for whole fruits), according to Hernández (2005). This test was carried out without removing the skin from the fruits.
In the case of guava, two maturation stages were evaluated on the first and third day of harvest, determining firmness at compression (N), 3% polar diameter (10 fruits per ripening stage), the contact area, (mm) and deformations of the polar and equatorial diameters, (mm) to obtain the modulus of elasticity, Poisson's coefficient and the elastic limit, according to González et al. (2015 and 2016).
Limit of elasticity: It was determined by using methodology proposed by Silling (2000), using a force meter (durometer model CEMA - C08 with a flat strut), a vernier caliper and a video camera. The average efforts of the fruits are determined through MATH CAD PRO 2000 program (Essential Mathcad for Engineering, Science, and Math (2000), which is based on the Equation 2.
σ=F/A, Mpa (2)
Young's Modulus or Apparent Elasticity Coefficient: It is determined according to Equation 3. The contact area is determined by marking the durometer plate with chalk powder, so, the area touching the fruit will be marked on it and subsequently obtained using a vernier caliper.
Where:- Maximum firmness to compression before breaking the fruit
- Deformation of the longitudinal diameter. Apparent Poisson Coefficient (μ) are quantified from Equation 4, and with the help of a caliper (Sharma et al., 2003; Ciro et al., 2005).
Since ΔD is the transverse deformation, Do the initial transverse length; with ΔL as longitudinal deformation and the initial longitudinal dimension, expressed in mm.
Where:- initial transverse length, mm
- longitudinal deformation
- initial longitudinal dimension, mm
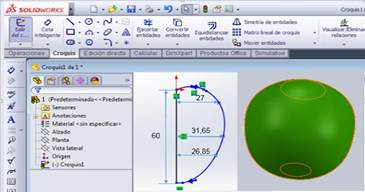
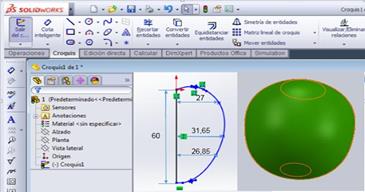
The simulation of static charges in a homogeneous body was made with the help of SolidWorks 2013 program. For the construction of the initial sketch (guava fruit), establishing average measurements (length and equatorial diameter), (Figure 1) in order to establish the appropriate geometry of the material. Once the solid is created, the program is fed with the physical and mechanical properties that characterize the fruit (density, Young's modulus, elasticity limit and Poisson's coefficient). Subsequently the analysis is performed by the Finite Element Method using two models, one for each state of maturation in terms of the deformations determined with the area of the plate-metal fruit and another one with the integrated area, in order to compare the simulated and experimental longitudinal deformations.
To evaluate the error of the model (EM) Equation 5 was used.
Where: - values of the predicted and measured variables, respectively.
RESULTS AND DISCUSSIONPineapple Properties: Table 1 shows the average values obtained in each of the main properties of quality evaluated in the case of pineapple, note that in this variety (Cayenne Lisa) the mass reached a maximum value of 927 g and a pH of 4.56.
TABLE 1
Average values obtained in the main pineapple quality properties.
| Properties of the Pineapple |
|---|
| Mass, g | Size, mm | Firmness, kgf/cm2 | IC* | SSC, 0Brix | pH | PP, g |
|---|
| 927 | 160 | 4.36 | -0,28 | 14.01 | 4.56 | 14,94 |
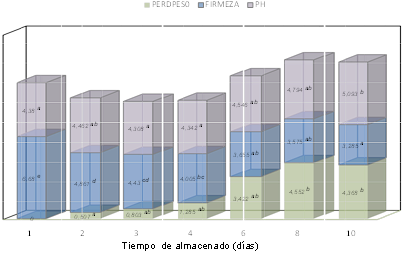
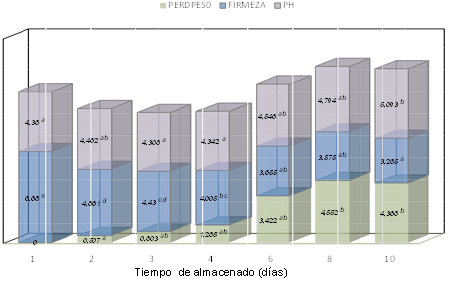
Results of Processing the Information Referred to Pineapple QualityAt the end of the evaluated period (Figure 2) weight losses (PP) are very significant, being those corresponding to the start and the second day of measurements, different from the eighth and tenth days (99% confidence level). As it can be seen, weight losses of intermediate days do not differ significantly from one or the other group of means. In the case of firmness, there is a decreasing trend with the days of storage. This is due to several changes that naturally accompany maturity in most fruits, among them the changes in texture and reduction of firmness. With senescence, phenomena such as the degradation of the walls, enzymatic activation, the increase in membrane permeability, among others, cause a decrease in the firmness of the walls of the fruit. The principal component analysis procedure then extracts or proposes five components, from which the first two components were chosen. The choice takes into account those self-values greater than or equal to 1.0 or, what is equal, the components that manage to explain more than 10% of the variance. These first and second CP explain 88% of the variability in the original data, which, as a whole, indirectly characterize the pineapple quality standards during post-harvest storage at room temperature. This result reaffirms that not only the well-known firmness, but weight loss, pH, IC and SSC are suitable indicators to qualify the quality of the fruit and also confirms its use for these purposes as a trend in the literature.
Multiple comparisons test applied to the properties to discern the groups of means that differ significantly during the storage time. Different letters indicate significant intergroup differences for p <0.01.
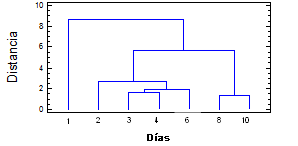
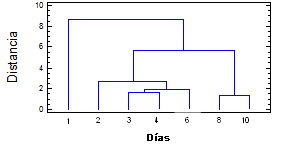
Figure 3 shows the conglomeration or grouping of variables practiced to weight loss, firmness, IC, pH and SSC with three well-defined resulting groupings, which are framed in specific days of storage of the fruit after harvest.
Cluster dendogram of weight loss, firmness, IC, pH and SSC generated considering the nearest neighbor method and the Euclidean distance squared.
The pattern of temporal quality variability of pineapple represented by these groupings properties is a valuable tool that excludes the need of carrying out an exhaustive control of these properties during its commercialization, transport or storage and even supplying the lack of instrumentation for their determination. This largely makes it a non-destructive tool to monitor the quality of the fruit in storage.
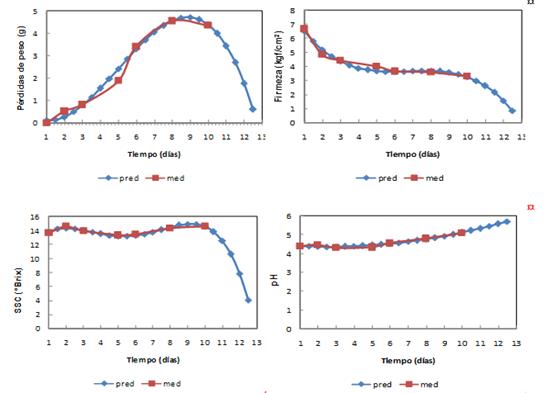
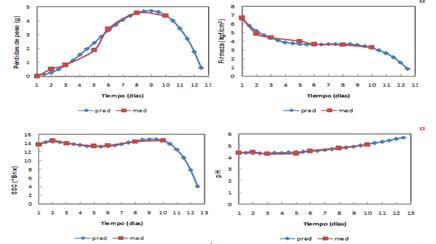
On the other hand, Figure 4 shows the models adjusted to the different tendencies or temporary variations of weight loss, firmness, SSC and pH, where both measured values are plotted during the ten days of storage and predicted by the models at half-day time intervals. In the case of the predicted values, these are extrapolated a few days later, which took into account not too far from the period of interest, as well as the temporal brevity of the process being analyzed. All the trends described by the models after ten days of storage are considered adequate and are result of the irreversible physiological changes that occur in the fruit, as can be seen with the rise in pH that is subject to the continuity of the fruit maturation.
Temporal trend of measured and predicted values with model adjusted for properties.
Table 2 shows the adjusted functional dependencies and the statistics that evaluate the adjustment of the model, reaching values of statistics as R2 statistic that indicates that the adjusted model is able to explain up to 99% of the temporal variability of weight losses. This model presents a standard error of the estimate of 0.23, which is why it is considered favorable to accurately describe the pineapple storage process at room temperature.
TABLE 2
Models adjusted to the values of each property and the statistics of its evaluation.
| Property | Model | R2 | MAE |
ES of estimating |
|---|
| PP | Y = 0,12-0,07*t+0,24*t2-0,02*t3 | 0,99 | 0,11 | 0,23 |
| Firmness | Y = 6,52-1,58*t +0,28*t2-0,02*t3 | 0,98 | 0,13 | 0,24 |
| SSC | Y = 13,79+1,25*t -0,83*t2+0,16*t3-0,01*t4 | 0,89 | 0,14 | 0,30 |
| pH | Y = 4,40-0,04*t +0,02*t2 | 0,97 | 0,04 | 0,06 |
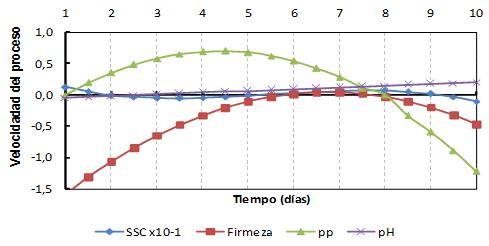
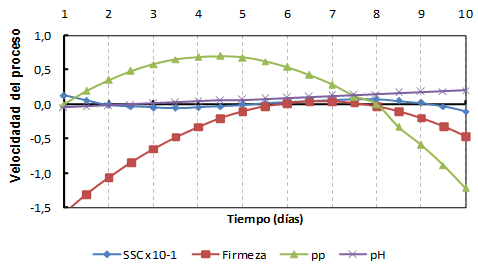
On the other hand, there is no tendency to represent the residues, which means that the variables taken into account are well represented in the model, as pointed out by Donatelli et al. (2004) and Borgesen and Schaap (2004) in the development of pedotransference functions to estimate the soil moisture retention curve. The speed with which the changes in each property measured during pineapple storage occur, can be seen in Figure 5. That graph shows the general dynamics of the processes that take place during the fruit storage at room temperature, particularized through the set of properties evaluated, which are closely related to pineapple maturation and quality (Var. Cayena Lisa). As it can be seen, the maximum speed of weight loss is reached between the fourth and fifth day of harvesting and stored at room temperature (0.7 g / day) and from sixth to seventh day the maximum for the firmness ( 0.04 kgf / cm2day). While the speed and average change rate during the entire storage period of these are 0.17 g / day and -0.04 kgf / cm2 day, respectively. In addition, the greatest degradations of the pineapple, in terms of quality, take place between the fourth and seventh day. The behavior of these properties (SSC and pH) are very contrasting to the previous ones (0.08 ° Brix and 0.08, respectively). Nevertheless, these extremes of the process, it is a gradual and cumulative phenomenon, so it should not be ignored or downplay the overall result.
Rate of change of properties during storage days.
Similar analyses to those of pineapple are made for the physical-mechanical properties of guava by states of maturation (Table 3). It also shows average diameters that make up the size of the fruit during the analysis and its classification according to size, as in the norm consulted NTC-1263: 2007, as well as the average values of mass and density.
TABLE 3
Average values of the main physical-mechanical properties of guava by states of
| | D polar, mm | D equatorial, mm | Mass, g | Classification | Den, g/cm3 |
|---|
| EM-I | 60.24 | 60.34 | 119.53 | Grande | 1.01 |
| EM-III | 63.24 | 61.3 | 152.48 | Grande | 0.96 |
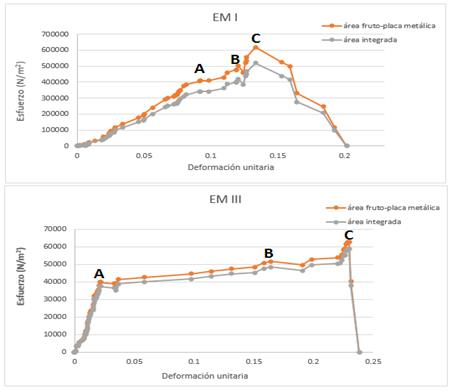
The changes of the firmness of guava, expressed as compression force (Table 4), is illustrative of those that occur in the ME that fruit transits through, coinciding with Hernández et al. (2005). As a whole, values reached of its elastic limit (point A), biocedencia point (point B), point of fracture (point C) and compression of the fruits up to 3% of its polar diameter are shown, and there is a significant difference between the MS.
TABLE 4
Average firmness of the fruits for each stage of maturation.
| Firmness (N) | EM-I** | EM-III** |
|---|
| Force at 3% (A) | 58,0 | 10,4 |
| Force (point A), | 531,5 | 49,0 |
| Force (point B), | 600,5 | 67,1 |
| Force (point C), | 804,8 | 81,9 |
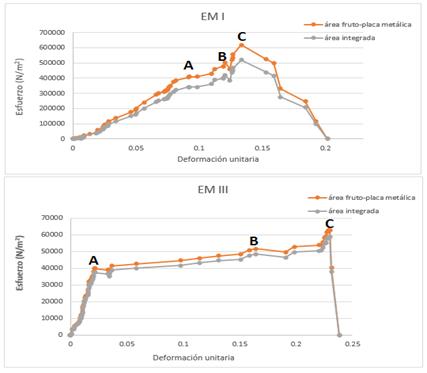
The stress-unitary deformation curves for each MS (Figure 6) for the fruit-metal plate area and the integrated area are plotted and its elastic limit is defined. From these curves the values of the elastic limit (A) are riched and the Young's Module by areas and EM. Table 5 shows their averages along with those of the Poisson coefficient obtained for each ME, which are used to characterize the material, and simulate the firmness of the fruits during the post-harvest stage in the SolidWorks 2013.
Stress - unitary deformation curves of guava in the maturation stages (EMI and EMIII).
According to the results obtained, it can be observed that as the fruits reach the EMIII, μ decreases because the material resistance decreases with the maturation, being more easily deformable for minor efforts. The values of the modulus of elasticity in the EM-I for the area fruit-metal plate and integrated area show remarkable changes of 4.44 to 3.71 MPa, not happening in the EM-III where the value for the fruit area - metal plate is 1.84 MPa and for the integrated area is 1.78 MPa.
TABLE 5
Physical-mechanical properties of guava fruits.
| Maturation State | Elasticity Limit, MPa | Elasticity Module, MPa | µ |
|---|
| EM-I (fruit-metal plate) | 0,41 | 4,44 | 0,34 |
| EM-I (integrated area) | 0,34 | 3,71 | 0,34 |
| EM-III (fruit-metal plate) | 0,13 | 1,84 | 0,49 |
| EM-III (integrated area) | 0,10 | 1,78 | 0,49 |
Simulation of Static Charges in a Homogeneous BodyThe generation of a mesh small enough to obtain reliable results is one of the most important steps in the simulation, since it must be able to solve the problem under study with a high precision and depends on a convergence analysis. The total number of nodes in this case was 10433 and the total number of elements 7045 (Figure 7).
Guava modeling with strength, restrictions and solid mesh.
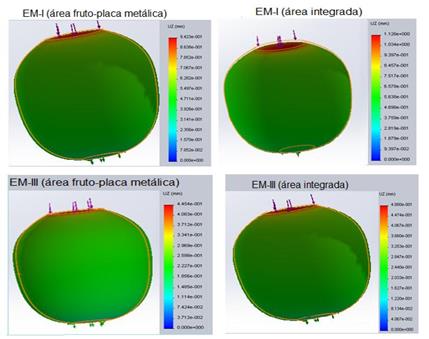
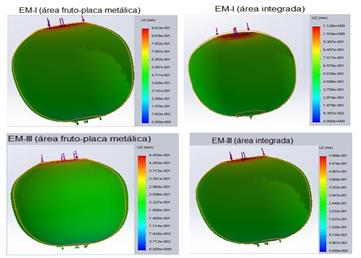
Figure 8 shows changes in the longitudinal deformations (mm), in the z direction, as the fruit moves from EMI to EM III. The fruit, in state of maturity one (EM-I), which is simulated with the modulus of elasticity that takes into account the fruit-metal plate area shows values of longitudinal deformation of 0.94 mm and the one that was simulated with the modulus of elasticity, assuming the integrated area of the fruit, reaches values of 1.12 mm, obtaining a simulation with the latter more approximate than the one obtained experimentally where values of 1.13 mm were recorded for a force of 58 N.
In the case of the state of maturation three (EM-III), for a load of 10.4 N, values of longitudinal deformation of 0.44 and 0.48 mm are obtained in fruits with fruit area-metal plate and integrated area, respectively. These values are closer to those obtained experimentally. In the opposite direction (equatorial diameter), the deformations are small, in the order of 1 to 2 mm, which does not represent a value to be taken into account with respect to those obtained in the contact zone between the fruits and the metal plates.
Result of the simulation of the longitudinal deformations when the fruit is compressed to 3% of the polar diameter in the two stages of maturation.
Comparison of the Results of the Experiment and the Numerical Analysis
Table 6 shows the comparison of both results (numerical analysis using the MEF and laboratory experiment), regarding the longitudinal deformations (ΔL) that occur with the application of compression loads for 3% of the polar diameter.
TABLE 6
Comparison of the average deformations obtained.
| EM | Fmax, N | DL, mm |
|---|
| Exp. | M E F |
|---|
| EM-I (fruit -metal plate area) | 58,0 | 1,15 | 0,94 |
| EM-I (integrated area) | 58,0 | 1,12 |
| EM-III (fruit area-metal plate) | 10,4 | 0,49 | 0,44 |
| EM-III (integrated area) | 10.4 | 0,48 |
To validate the model, it is necessary to determine the prediction errors of the model, in each of the analyzed variables, where the experimentally obtained values are compared with those derived from the evaluation of the digital model. It can be observed that, in all the states of maturation, a precision of the model greater than 80% is obtained, and in those corresponding to the model (integrated area), it is greater than 90%, table 7.
TABLE 7
Estimating model errors for deformation.
| EM | Charge, N | Error of deformation,% | Error of model,% |
|---|
| EM-I (fruit -metal plate area) | 58 | 18,26 | 81,74 |
| EM-I (integrated area) | 58 | 2,60 | 97,4 |
| EM-III (fruit -metal plate area) | 10,4 | 10,20 | 89,8 |
| EM-III (integrated area) | 10,4 | 2,04 | 97,96 |
CONCLUSIONS
With the use of mathematical and simulation techniques, the behavior of properties in pineapple are described and the maximum effort that guava fruit resists in two stages of maturation under static loads, is predicted.
The quality pattern of Cayenne pineapple, stored at room temperature, quantified from weight loss, firmness, pH, contents of soluble solids and color index, is distinguished by three periods corresponding to initial day, between two and six days and between seven and ten days of fruit storage.
The average speed or rate of change of pineapple weight and firmness losses are 0.17 g / day and -0.04 kgf / cm2 / day, respectively, during the entire ten-day storage period at room temperature, while that of the pH and contents of soluble solids is, in both cases, of only 0.08 units per day.
Guava as fresh fruit has average values of height, density and Poisson's coefficient of 60 ± 5 mm, 0.98 g / cm3, 0.41, respectively.
In the module of fruit elasticity in EM-I (fruit -metallic plate area and integrated area) remarkable changes of 4.44 to 3.71 MPa are shown, which do not happen in EM-III, where the values for the fruit-metal plate area is 1.84 MPa and the integrated area is 1.78 MPa.
INTRODUCCIÓNLlevar a cabo la conservación adecuada en la etapa poscosecha de los productos se encuentra entre los principales pasos encaminados a lograr soberanía alimentaria y a mejorar la eficiencia en el uso de las producciones agropecuarias, lo cual solo es posible si se tiene un producto de calidad con un elevado grado de aceptación (Hernández et al., 2005; García y Hernández, 2007; Mogollón et al., 2011; Fernández et al., 2012; Ramos Hernández et al., 2013; Jiménez, 2015; López, 2017). La calidad de los productos agrícolas no es más que una serie de atributos relacionados fundamentalmente con su sanidad general y con su vida comercial. El conocimiento de las principales propiedades físico- mecánicas y organolépticas empleando métodos tradicionales y más recientemente los no destructivos, juega un papel indispensable para una buena presentación y conservación de los mismos, permitiendo definir el manejo más adecuado durante los periodos de pre-cosecha, cosecha y poscosecha (Schofield y Wroth, 1968; Yirat Becerra et al., 2009; Mogollón et al., 2011; Jiménez, 2015; López, 2017). Los no destructivos tienen la posibilidad de ser utilizados para la automatización de los procesos de selección en línea y en el desarrollo de la investigación científica a partir de que es posible homogeneizar el criterio de selección de muestras para estudios donde intervienen varias cualidades del fruto y que históricamente se realizaban auxiliándose del criterio de expertos. (FAO, 2018).
En los últimos años, como consecuencia del desarrollo de la electrónica y la informática, se ha avanzado considerablemente en el uso de técnicas matemáticas(Regresión Lineal Múltiple, Regresión de los Componentes Principales, Mínimos Cuadrados Parciales entre otros) estas aplicaciones con fines docentes e investigativos ,lo que queda demostrado en la propuesta en la que se retoma los estudios de calidad aplicados a frutos a partir de nuevas formas y métodos devenidos del desarrollo tecnológico, como son los relacionados con la modelación y simulación de frutos o procesos que se suceden esencialmente durante la etapa de la poscosecha, lo que propicia realizar mediciones menos engorrosas y más precisas, posibilitando además el monitoreo no destructivo de este importante atributo para frutas en estado fresco, durante su almacenamiento a temperatura ambiente (Park et al., 2001; García y Hernández, 2007).
Por otro lado el MEF ha sido ampliamente utilizado(Silvestre, 1998; Nourain et al., 2005; Lu et al., 2006; Kabas et al., 2008) para caracterizar la respuesta de productos agrícolas sometidos a cargas estáticas, durante el almacenamiento y transportación de los mismos por periodos de tiempo relativamente largos, demostrando su eficacia en verificaciones no destructivas a los frutos.
En las últimas tres décadas el método ha sido aplicado en Cuba con éxito en el campo de la ingeniería agrícola, fundamentalmente en la modelación de la interacción suelo - implemento agrícola (Herrera et al., 2008; Martínez et al., 2011; López, 2017). Por todo lo antes expuesto es que la investigación tiene como objetivo Emplear técnicas matemáticas y de simulación para describir el comportamiento de las propiedades en piña y predecir el esfuerzo máximo que resiste el fruto de la guayaba en dos estados de maduración bajo cargas estáticas.
MATERIALES Y MÉTODOSMediante la Norma Mexicana (Norma Técnica Mexicana NMX-FF-041-SCFI-2007, 2007), se llevó a cabo la selección de los frutos de la guayaba (enana roja) y la piña (cayena lisa. Se muestreo un total de 110 frutas (40 guayabas y 70 piñas). En el caso de la piña, se retiraron 10 frutos diariamente, durante los días experimentales y para el caso de la guayaba se dividen en dos grupos por estados de maduración (escogiéndose solo dos estados debido a que la fruta suele recogerse para su exportación en el estado uno (verde) y suele ser más susceptible a daños en el estado III (maduro), de ahí que sean los de mayor interés, conformados por 20 frutos cada uno. De los 20 frutos por cada uno de los estados se dividen en 10 para determinar masa, densidad, firmeza a la compresión al 3% del diámetro polar (Ф), y 10 para la determinación del límite de elasticidad, módulo de Young y coeficiente de Poisson.
La talla se obtiene mediante el diámetro polar y ecuatorial con la utilización de un calibrador pie de rey de 0 a 150 mm ± 0.05 mm. La
masa
se determina con una balanza electrónica modelo LG-1001a/ 0,1 (g), realizando tres repeticiones por fruto y determinándose las pérdidas de peso mediante la ecuación. 1. El IC se determinó por el método de captación de imágenes, fotografiando las frutas con una cámara digital modelo CANON PowerShot A630 8.5 mega-píxeles, luego exportadas al software portable ADOBE PHOTOSHOP v.10, obteniendo la representación numérica de las variables L* a* y b*, el cual establece coordenadas en un plano de colores que establece por sus coordenadas la escala de maduración (García, et al., 2010).
donde:- peso de la fruta en el día cero, g;
- peso de la fruta en el día de interés, g.
Se evalúa los contenidos de sólidos solubles (SSC, por sus siglas en ingles) y la densidad se determina a través del principio de Arquímedes.
Resistencia a la penetración (firmeza): se obtuvo a partir de la prueba del pinchazo para el caso de la piña y a la compresión al 3% del diámetro polar en el caso de la guayaba, con el durómetro digital, Modelo CEMA-C08, 0 a 1000 (kgf/cm2)/0,01 (kgf/cm2), de fabricación nacional, según principio Magness-Taylor en tres puntos equidistantes, separados a 120º aproximadamente unos de otros (para los frutos enteros), según (Hernández et al., 2005a). Esta prueba se realizó sin quitarle la piel a las frutas.
Para el caso de la guayaba se evaluó dos estados de maduración al primer y tercer día de cosechada, determinándose la firmeza a la compresión (N), al 3% del diámetro polar (10 frutos por estado de maduración), el área de contacto, (mm) y deformaciones del diámetro polar y ecuatorial, (mm) para obtener el módulo de elasticidad, coeficiente de Poisson y el límite elástico, teniendo en cuenta investigaciones precedentes (González et al., 2016).
Límite de elasticidad: Se determina utilizando la metodología propuesta por Silling (2000), utilizando un medidor de fuerza (durómetro modelo CEMA - C08 con un puntal plano), pie de rey y una videocámara. Los esfuerzos medios de los frutos se determinan, a través del programa MATH CAD PRO 2000 (Essential Mathcad for Engineering, Science, and Math (2000), que se apoya en la ecuación. 2
σ=F/A, Mpa (2)
Módulo de Young o Coeficiente de Elasticidad aparente: Se determina de acuerdo a ecuación. 3. El área de contacto se determina marcando el plato del durómetro con polvo de tiza para que el área que toca a la fruta quedara marcada en esta y posteriormente se obtiene utilizando un pie de rey.
donde:- Firmeza máxima a la compresión antes de romper el fruto
- Deformación del diámetro longitudinal
Coeficiente de Poisson aparente (µ): se cuantifican a partir de la ecuación. 4, auxiliándonos de un pie de rey (Turner et al., 1956; Schofield y Wroth, 1968) (Ciro y Osorio, 2005).
donde:- deformación transversal
- Longitud transversal inicial, mm
- deformación longitudinal
- dimensión longitudinal inicial, mm
La simulación de cargas estáticas en un cuerpo homogéneo: se realizó con la ayuda del programa SolidWorks (2013). Para la construcción del boceto inicial (fruta de guayaba), estableciendo unas medidas promedio (longitud y diámetro ecuatorial), (Figura 1) con el fin de establecer la geometría apropiada del material. Una vez creado el sólido, se procede a alimentar el programa con las propiedades físicas y mecánicas que caracterizan la fruta; densidad, módulo de Young, límite de elasticidad y Coeficiente de Poisson. Posteriormente se realiza el análisis mediante el Método de Elemento Finito empleando dos modelos, uno para cada estado de maduración en cuanto a las deformaciones determinadas con el área del fruto placa-metálica y otro con el del área integrada, con el objetivo de comparar las deformaciones longitudinales simuladas y experimentales.
Para evaluar el error del modelo (EM) se emplea la ecuación. (5)
donde:- valores de las variables predichos y medidos, respectivamente.
RESULTADOS Y DISCUSIÓNPropiedades de la Piña: La Tabla 1 muestra los valores promedios obtenidos en cada una de las principales propiedad de la calidad evaluadas en el caso de la piña, señalar que en esta variedad (Cayena Lisa) la masa alcanzo como valor máximo de 927 g y un pH de 4.56.
TABLA 1
Valores promedios obtenidos en las principales propiedades de calidad de la piña
| Propiedades de la Piña |
|---|
| Masa, g | Talla, mm | Firmeza, kgf/cm2 | IC* | SSC, 0Brix | pH | PP, g |
|---|
| 927 | 160 | 4.36 | -0,28 | 14.01 | 4.56 | 14,94 |
Resultados del procesamiento de la información referida a la calidad de la piñaAl final del periodo evaluado (Figura 2) las pérdidas de peso (PP) son muy significativas, siendo las correspondientes al inicio y al segundo día de mediciones diferentes al del octavo y décimo día (nivel de confianza del 99%). Como se puede apreciar las pérdidas de peso de días intermedios a estos no difieren significativamente de uno u otro grupo de medias. En el caso de la firmeza se manifiesta una tendencia decreciente con los días de almacenamiento. Ello obedece a varios cambios que acompañan de modo natural a la madurez en la mayoría de las frutas, entre ellos se destaca los cambios en textura y reducción de la firmeza. Con la senescencia los fenómenos como la degradación de las paredes, activación enzimática, el aumento de la permeabilidad de membranas, entre otros provocan una disminuyen de la firmeza de las paredes del fruto. El procedimiento de análisis de componentes principales seguido extrae o propone cinco componentes, de las cuales se eligieron las dos primeras de ellas. La elección tiene en cuenta aquellos auto-valores mayores o iguales a 1,0 o lo que es igual las componentes que logran explicar más del 10% de la varianza. Estas primera y segunda CP explican el 88% de la variabilidad en los datos originales, las cuales en su conjunto caracterizan indirectamente los estándares de calidad de la piña durante su almacenamiento postcosecha a temperatura ambiente. Este resultado viene a reafirmar que no solo la muy conocida firmeza, sino que las pérdidas de peso, el pH, el IC y los SSC son indicadores adecuados para calificar la calidad de la fruta y también confirma su uso con estos fines como tendencia en la literatura.
Prueba de comparaciones múltiples aplicadas a las propiedades para disernir los grupos de medias que difieren significativamente durante el tiempo de almacenamiento. Letras diferentes indican diferencias significativas intergrupos para un p < 0,01.
La Figura 3 muestra la conglomeración o agrupamiento de variables practicado a las pérdidas de peso, la firmeza, el IC, pH y SSC con tres agrupamientos resultantes bien definidos, los cuales se enmarcan en días específicos de almacenamiento de la fruta después de su cosecha.
Dendograma de clústers de las pérdidas de peso, la firmeza, el IC, pH y SSC generados considerando el método del vecino más cercano y la distancia Euclídeana al cuadrado.
La calidad de la piña representada por estos agrupamientos de principales propiedades constituye una valiosa herramienta estadística que nos exonera de llevar a cabo un control exhaustivo de las mismas sobre todo para la comercialización, transporte o almacenaje.
La Figura 4 muestra los modelos ajustados a las distintas variaciones temporales de cada propiedad estudiada en el fruto de la piña, graficando tanto sus valores medidos durante los diez días de almacenados como lo predichos por intervalos de tiempo de medio día. Todas las tendencias descritas por los modelos con posterioridad a los diez días de almacenado se consideran adecuadas y están en consecuencias a los cambios fisiológicos irreversibles que se suceden en la fruta, como se puede apreciar con el ascenso del pH que está sujeto a la continuidad de la maduración del fruto.
Tendencia temporal de valores medidos y predichos con modelo ajustado por propiedades.
La Tabla 2 muestra las dependencias funcionales ajustadas y los estadísticos que evalúan el ajuste del modelo, alcanzándose valores de estadígrafos como el estadístico R2 que indica que el modelo ajustado es capaz de explicar hasta un 99% de la variabilidad temporal de las pérdidas de peso. Este modelo presenta un error estándar de la estimación es de 0,23, por lo que se considera favorable para describir certeramente el proceso de almacenamiento de la piña a temperatura ambiente.
TABLA 2
Modelos ajustados a los valores de cada propiedad y los estadísticos de su evaluación
| Propiedad | Model | R2 | MAE |
ES de estimación |
|---|
| PP | Y = 0,12-0,07*t+0,24*t2-0,02*t3 | 0,99 | 0,11 | 0,23 |
| Firmeza | Y = 6,52-1,58*t +0,28*t2-0,02*t3 | 0,98 | 0,13 | 0,24 |
| SSC | Y = 13,79+1,25*t -0,83*t2+0,16*t3-0,01*t4 | 0,89 | 0,14 | 0,30 |
| pH | Y = 4,40-0,04*t +0,02*t2 | 0,97 | 0,04 | 0,06 |
Por otra parte, no se observan tendencia al representar los residuos, lo cual se traduce en que las variables tomadas en cuenta están bien representadas en el modelo, tal y como lo enfocan Donatelli et al. (2004; Børgesen y Schaap (2005), en el desarrollo de funciones de pedotransferencia para estimar la curva de retención de humedad de suelo.
La velocidad con que suceden los cambios en cada propiedad medidas durante el almacenamiento de la piña se puede apreciar en la Figura 5, donde la gráfica evidencia la dinámica general de los procesos que se suceden durante el almacenamiento del fruto a temperatura ambiente, particularizadas a través del conjunto de propiedades evaluadas, las cuales se relacionan estrechamente con la maduración y calidad de la piña (Var. Cayena Lisa). Como se aprecia la máxima velocidad de las pérdidas de peso se alcanza entre el cuarto y quinto día de cosechado y almacenado a temperatura ambiente (0,7 g/día) y a partir sexto y hasta el día siete se suceden las máximas para la firmeza (0,04 kgf/cm2 día). Mientras que la velocidad o razón de cambio promedio durante todo el periodo de almacenamiento de estas son de 0,17 g/día y -0,04 kgf/cm2día, respectivamente. Además de ello, las mayores degradaciones de la piña en términos de calidad tienen lugar entre el cuarto y séptimo día. El comportamiento de estas propiedades (SSC y pH) son muy contrastantes a las anteriores (0,08° Brix y 0,08, respectivamente). No obstante, estos extremos del proceso, se trata de un fenómeno paulatino y acumulativo, por lo cual no ha de obviarse ni restar importancia al resultado global.
Velocidad de cambio de las propiedades durante los días de almacenamiento.
Similares análisis a los de la piña se realizan para las propiedades físico-mecánicas de la Guayaba por estados de maduración (Tabla 3). Los diámetros promedios que conforman la talla de las frutas durante el análisis y su clasificación de acuerdo al tamaño, según la norma consultada (Norma Técnica Colombiana NTC 1263, 2007), así como los valores medios de la masa y la densidad.
TABLA 3
Valores promedios de las principales propiedades físico-mecánicas de la guayaba por estados de maduración (EM)
| | D polar, mm | D ecuatorial, mm | Masa, g | Clasificación | Den, g/cm3 |
|---|
| EM-I | 60.24 | 60.34 | 119.53 | Grande | 1.01 |
| EM-III | 63.24 | 61.3 | 152.48 | Grande | 0.96 |
Los cambios de la firmeza de la guayaba, expresada como fuerza de compresión (Tabla 4), es ilustrativo de los que se suceden en los EM que transita la fruta, coincidiendo con (Hernández et al., 2005a). De conjunto se muestran valores alcanzados de su límite elástico (punto A), punto de biocedencia (punto B), l punto de fractura (punto C) y la compresión de los frutos hasta el 3% de su diámetro polar, existiendo diferencia significativa entre los EM.
TABLA 4
Firmeza promedio de las frutas por cada estado de maduración
| Firmeza promedio (N) | EM-I** | EM-III** |
|---|
| Fuerza al 3% (N) | 58,0 | 10,4 |
| Fuerza con que alcanza el punto (A), (N) | 531,5 | 49,0 |
| Fuerza con que alcanza el punto (B), (N) | 600,5 | 67,1 |
| Fuerza con que alcanza el punto (C), (N) | 804,8 | 81,9 |
Las curvas de esfuerzo-deformación unitaria para cada EM (Figura 6) para el área fruto- placa metálica y el área integrada y así definir su límite elástico. De dichas curvas se llega a los valores del límite elástico (A) y del Módulo de Young por áreas y EM. La Tabla 5 muestra sus promedios de los mismos junto con los del coeficiente de Poisson obtenidos para cada EM, las cuales se utilizan para caracterizar el material, y simular la firmeza de las frutas durante la etapa poscosecha en el programa de cómputo SolidWorks (2013).
Curva de esfuerzo - deformación unitaria de la guayaba en los estados de maduración (EMI Y EMIII).
De acuerdo a los resultados obtenidos se puede observar que a medida que los frutos alcanzan el EMIII decrece en el µ debido a que la resistencia del material disminuye con la maduración, siendo más fácilmente deformable para esfuerzos menores. Los valores del módulo de elasticidad en el EM-I para el área fruto-placa metálica y área integrada se muestran cambios notables de 4,44 a 3,71 MPa, no ocurriendo así en el EM-III donde los valores para el área fruto-placa metálica son de 1,84 MPa y el área integrada son de 1,78 MPa.
Tabla 5
Propiedades físico-mecánicas de las frutas de guayaba.
| Estado de maduración | Límite de elast., MPa | Módulo de Elast., MPa | µ |
|---|
| EM-I (fruto-placa metálica) | 0,41 | 4,44 | 0,34 |
| EM-I (área integrada) | 0,34 | 3,71 | 0,34 |
| EM-III(fruto-placa metálica) | 0,13 | 1,84 | 0,49 |
| EM-III (área integrada) | 0,10 | 1,78 | 0,49 |
Simulación de cargas estáticas en un cuerpo homogéneoLa generación de una malla lo suficientemente pequeña para obtener resultados confiables es uno de los pasos más importantes en la simulación, ya que la misma debe ser capaz de resolver el problema en estudio con una alta precisión y depende de un análisis de convergencia por ello el número total de nodos en este caso fue de 10 433 y el número total de elementos 7045 (Figura 7).
Modelación de la guayaba con la fuerza, restricciones y malla sólida.
En la Figura 8 ocurren cambios en las deformaciones longitudinales (mm), en la dirección z, a medida que el fruto pasa del EMI al EM III. El fruto, en estado de madurez uno (EM-I), que se simulo con el módulo de elasticidad que tiene en cuenta el área fruto-placa metálica muestra valores de deformación longitudinal de 0,94 mm y el que se simulo con módulo de elasticidad asumiendo el área integrada de la fruta alcanza valores de 1,12 mm, obteniendo una simulación con este último más aproximada al obtenido experimentalmente donde se registraron valores de 1,13 mm para una fuerza de 58 N.
En el caso del estado de maduración tres (EM-III) se tienen para una carga de 10,4 N valores de deformación longitudinal de 0,44 y 0,48 mm, en los frutos con área fruto-placa metálica y área integrada respectivamente, siendo estos valores más aproximados a los obtenidos experimentalmente. En la dirección contraria (diámetro ecuatorial) las deformaciones son pequeñas del orden de 1 a 2 mm lo cual no representa un valor a tener en cuenta con respecto a los obtenidos en la zona de contacto entre las frutas y las placas metálicas.
Resultado de la simulación de las deformaciones longitudinales al comprimirse el fruto al 3% del diámetro polar en los dos estados de maduración.
Comparación de los resultados del experimento y el análisis numérico: en l
a Tabla 6, se muestra la comparación de ambos resultados (análisis numérico mediante el MEF y experimento de laboratorio), en cuanto a las deformaciones longitudinales (ΔL) que se produce con la aplicación de las cargas de compresión para el 3% del diámetro polar.
TABLA 6
Comparación de las deformaciones medias obtenidas
| Estados de Madurez(EM) | Fmáx, N | Deformaciones longitudinales, mm |
|---|
| Exp. | M E F |
|---|
| EM-I(área fruto-placa metálica) | 58,0 | 1,15 | 0,94 |
| EM-I (área integrada) | 58,0 | 1,12 |
| EM-III(área fruto-placa metálica) | 10,4 | 0,49 | 0,44 |
| EM-III (área integrada) | 10.4 | 0,48 |
Para realizar la validación del modelo es preciso determinar los errores de predicción del mismo, en cada una de las variables analizadas, donde se comparan los valores obtenidos experimentalmente con los derivados de la evaluación del modelo digital. En la misma se puede observar que en todos los estados de maduración se obtiene una precisión del modelo mayor al 80%, y en los correspondientes al modelo (área integrada) mayor al 90%, tabla 7.
TABLA 7
Estimación de errores del modelo para la deformación
| EM | Carga, N | Error de deformación,% | Error de modelo,% |
|---|
| EM-I (área fruto-placa metálica) | 58 | 18,26 | 81,74 |
| EM-I (área integrada) | 58 | 2,60 | 97,4 |
| EM-III (área fruto-placa metálica) | 10,4 | 10,20 | 89,8 |
| EM-III (área integrada) | 10,4 | 2,04 | 97,96 |
CONCLUSIONES
Con el empleo de técnicas matemáticas y de simulación para describir el comportamiento de las propiedades en piña y predecir el esfuerzo máximo que resiste el fruto de la guayaba en dos estados de maduración bajo cargas estáticas.
En el patrón de calidad de la piña Cayena Lisa almacenada a temperatura ambiente, cuantificado a partir de las pérdidas de peso, la firmeza, el pH, los contenidos de sólidos solubles y su índice de color, se distingue por tres períodos correspondientes al día inicial, entre dos y seis días y entre los siete y diez días de almacenamiento de la fruta.
La velocidad o razón de cambio promedio durante todo el periodo de almacenamiento de diez días a temperatura ambiente de las pérdidas de peso y la firmeza de la piña son de 0,17 g/día y -0,04 kgf/cm2día, mientras que las del pH y los contenidos de sólidos solubles es en ambos casos de apenas 0,08 unidades por día.
La guayaba como fruta fresca posee valores medios de talla, densidad y coeficiente de Poisson de 60 ±5 mm, 0,98 g/cm3, 0,41, respectivamente.
En el módulo de elasticidad de los frutos en EM-I (área fruto-placa metálica y área integrada) se muestran cambios notables de 4,44 a 3,71 MPa, no ocurriendo así en el EM-III donde los valores para el área fruto-placa metálica son de 1,84 MPa y el área integrada son de 1,78 MPa.