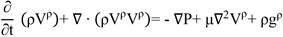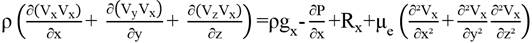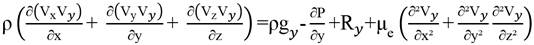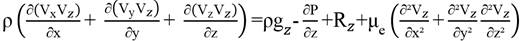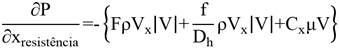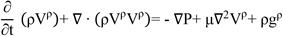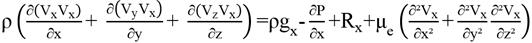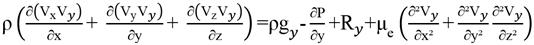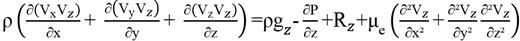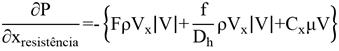Translate PaperORIGINAL ARTICLE http://opn.to/a/CbobL
http://opn.to/a/CbobLStatic Pressure Drop across a Bed of Coffee Beans: Finite Element Analysis
[*] Correspondence to author: Filipe da Silva de Oliveira. e-mail: filipe.oliveira@posgrad.ufla.br
ABSTRACTSeveral are the post-harvest processes of agricultural products in which a fluid flows through a fixed bed of particles. Therefore, the objective of this work was to model the static pressure drop in a bed filled with coffee beans (Coffea arábica L.) with different water contents, submitted to different airflows. The pressure drop results using the finite element technique were satisfactorily adjusted to the data obtained by a classical method, where the pressure drop along the elevation of the coffee column varied linearly between 158.8 and 455.6 Pa, for the column depths of 0.45 and 0.95 m, respectively. The relative error, by this technique remained below 5 %, for all samples. The distributed resistance had an average of 7,2 x 107 m-2, with an average relative error of 0.3 %, for all treatments considered.
INTRODUCTIONIn order to achieve efficient storage of bulk agricultural grains, the product must undergo drying and aeration operations. The adequate execution of these processes prolongs the storage period and avoids the deterioration of the product, which results from its biological activity.
Thus, a mass of air is generally forced to pass through the agricultural product; the air, finding resistance of the granular product to its passage, flows through the intergranular spaces. The determination of the resistance to the air flow for agricultural products can be measured by the drop of pressure, being fundamental in projects of drying and aeration systems ((Brandão et al., 2016; Korese et al., 2016; Olatunde et al., 2016; Gao et al., 2018).
The resistance to airflow in drying and aeration systems depends on several factors, such as: air flow intensity, grain layer height, impurities in the product, size, shape, moisture content, grain distribution in the mass granular, and roughness of the product (Brooker et al., 1992).
The method of filling the grain column, its compaction, and the direction of the air flow influence the resistance of a product to the passage of air flow. In these systems, perforated plates, perforated ducts and pipelines are responsible for an increase in pressure drop (Gratão et al., 2013; Teixeira et al., 2015).
Corrêa et al. (2001) studied the effects of airflow density, size and quantity of impurities on the static pressure drop in granular bean masses and adjusted the basic empirical mathematical models according to the data obtained. Other researchers studied the variation of static pressure along a column of dried husk of coffee cherry, as a function of air flow density, moisture content, apparent specific mass, and product layer depth (Afonso, 1994).
Theoretically, the problem of fluid flow is defined by the laws of mass, momentum, and energy conservation. When the following constraints are considered: (a) the fluid is Newtonian, (b) the fluid is incompressible, (c) there is no phase change, (d) the flow is isothermal and permanent, (e) the spatial domain of the problem does not change over time and (f) the viscosity of the fluid is constant, the Navier-Stokes equation is given by Equation 01.
Thus, Equation 01 can be rewritten as a function of the components x, y and, z (Equation 02).
Several researchers have experimentally determined the pressure drop in columns of agricultural products (Iqbal et al., 2015, Dilmac et al., 2016, Du et al., 2016 and Horabik et al., 2016).
In addition, other researchers have studied expressing the pressure gradient as a function of the airflow imposed on a column of grains (Shedd, 1953; Hukill and Ives, 1955; Haque et al., 1978; Hunter, 1983; Giner and Denisienia, 1996).
Numerical techniques have been widely used in solving problems of fluid flow. Among them, the technique of finite elements has been used with success by the researchers for the resolution of different problems, involving drainage of air in agricultural products, such as the drying (Beigi, 2017, Chiang et al., 2017and Lemus-Mondaca et al.,2017). And for the distributed resistance others have also used it (De Andrade et al., 2001, Khatchatourian and Savierscki, 2004, Devilla et al., 2005, Yue and Zhang, 2014 and Moses et al., 2015).
Thus, the general objectives of this work were (1) to analyze, through the finite element technique, the static pressure drop in a bed filled with coffee, submitted to different air flows and water contents; (2) to determine the permeability of the bed to the different air flows and water contents.
METHODSParticle Bed and AirflowThe pressure drops were simulated in a duct of circular cross-section (0.3050 m diameter) with a length of 1.00 m, vertically positioned. The duct was filled with grains of Coffea arabica L. (cv Catuaí). To analyze the effect of moisture content on the resistance to airflow, two samples of clean grains were conditioned to the following moisture levels: 12.7 and 23.5% w.b. The imposed airflows at the entrance of the bed were 0.165, 0.253 and 0.263 m3 s-1 m-2.
Finite Element AnalysisThe determination of the profile of pressure and velocity in problems of fluid flow in ducts without particles was obtained through the finite element technique assisted by interactive software for analyzing systems, ANSYS®, commercially available.
The input files, which were considered for the computational programs developed, were the properties of the fluid, the boundary conditions on all open or closed surfaces of the system, and the type of analysis to be performed. The contour conditions on opened surfaces were the velocity, pressure or combinations of these parameters; as a result, the velocity and pressure distributions at the nodes from the discretization of the system were obtained.
In this work, the software ANSYS 15.0 was used to develop a source program that performs a three-dimensional analysis of the airflow in a fixed column of coffee beans. The product inside the column was considered equivalent to a distributed resistance inside the duct, which correspond to the terms Rx, Ry and Rz, in Equations (2a-b-c).
Therefore, the geometry of the porous medium was disregarded. Then, the flow resistance was modeled as a distributed resistance. As observed in Equation (03), such resistance may be due to one or a combination of the following factors: a localized loss of pressure (F); a friction factor (f) or a factor (C) related to the permeability (K) where C = 1 / K. Thus, the total pressure gradient, in the x direction, can be expressed by ANSYS (2013):
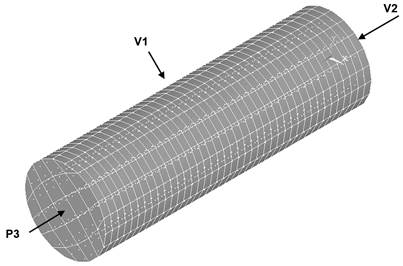
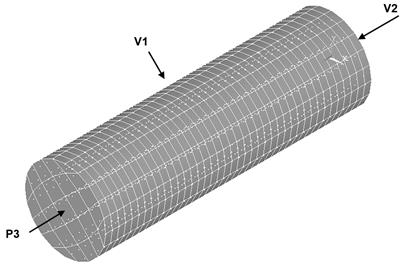
The duct was divided into 1440 elements of type FLUID142, with eight nodes, resulting in 1927 nodes at the end of the discretization, as shown in Figure 1. The inputs of the source program were the air properties (assumed constant), the value of C, referred to in the text as RD1 (distributed resistance) and boundary conditions, which, by the structure of the computational program, were imposed on all surfaces, open or closed, that delimited the medium being investigated.
Mesh and boundary conditions for finite element analysis.
Therefore, boundary conditions were: (1) zero velocities (V1), according to the three coordinate axes, on the inner side wall of the duct; (2) constant and evenly distributed velocity (V2) at the base of the duct, and (3) pressure (P3) equal to zero (reference) at all nodes at the upper end of the duct.
Comparison of ModelsTo describe the behavior of the static pressure as a function of the water content, column depth and flow density for the pulped coffee without impurities, the pressure drop of the air flowing through a column of coffee beans, determined by the finite element technique, were compared to those from the coefficients of the quadratic equations adjusted. (Da Silva et al., 2006)
The authors found that the actual specific mass, apparent specific mass and porosity for the pulped coffee with water content of 12.7% were 0.7929 g cm -3, 0.3879 g cm -3 and 51, 59%, respectively. While samples with 23.5% w.b. had 0.8685 g cm-3, 0.4635 g cm-3 and 48.35%, respectively (Table 1). The validity of the model proposed by the authors is for depths ranging from 0.00 to 0.95 m and for flows between 0.16 and 0.26 m3 s-1 m-2.
TABLE 1
| Coefficients | a | b | c | d | e | f | g | h | i | j |
|---|
| -1,31 | 0 | 95,71 | 27,63 | -651,14 | 1.202,38 | 6,62 | 1.355,89 | -1,26 | 83,23 |
RESULTS AND DISCUSSION
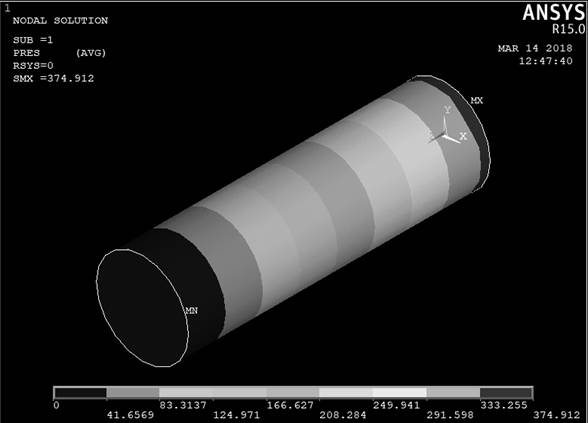
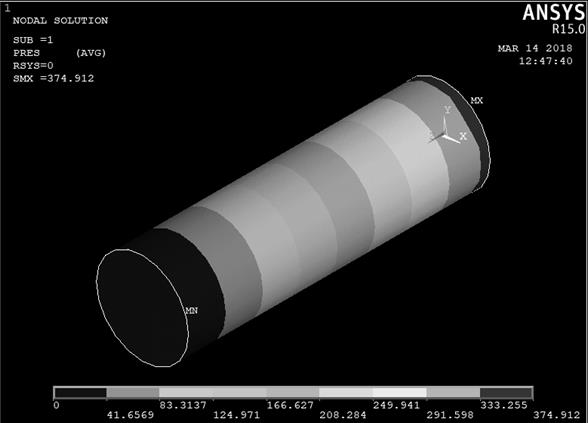
Figure 2 presents the contour plot of the static pressures of the sample with 12.7% of water content, without impurity and with air flow of 0.165 m3 s-1 m-2, simulated by ANSYS. It can be observed that along the column, from the axis of the coordinates (X, Y, Z), the values obtained decrease. According to the simulated data, the maximum and minimum pressures in the column are located, respectively, in the coordinate axis and at the top of the column, being 374.9 Pa and 0 Pa.
Nodal solution of the coffee pulped with water content in 12,7% b.u. and airflow in 0,165 m3∙s-1∙m-2.
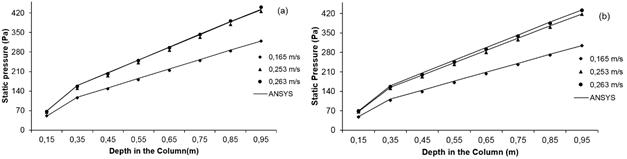
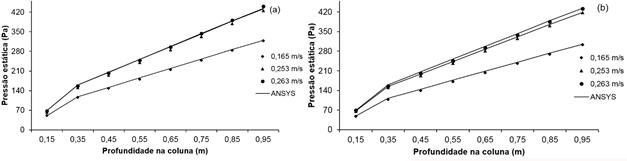
The simulations of the pressure variations at different depths of a column of coffee pulped with water content in 12.7% b.u. for different air flows are shown in Figure 3 (a), and for samples with water content of 23.5% b.u., the results are shown in Figure 3 (b).
Pressure drop as a function of depth in a column of coffee pulped with water contents of (a) 12,7% w.b. and (b) 23,5% w.b, for different airflows (m3 s-1 m-2).
It could be observed that the density of the airflow is directly related to the resistance of the airflow, as well as to the depth in the coffee column. As expected, static pressure values increase with increasing density of airflow applied to the mass. On the other hand, no difference in static pressure was observed between treatments with different water contents of the pulped coffee analyzed.
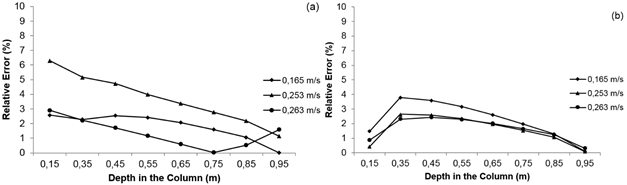
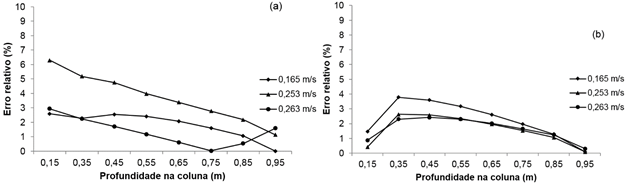
The relative percentage errors corresponding to the pressure drops obtained by the simulation are presented in Figure 4 (a), for samples with water content of 12.7% and in Figure 4 (b), for samples with water content of 23.5 %. It is seen in Figure 4 that the relative error values decrease the extent to which the product layer is increased, which is in agreement with the data obtained by Moses et al. (2014a, 2014b, 2014c).
Relative errors involved in the simulated values for the pressure drop in the depths of coffee beans with water contents of (a) 12.7% w.b. and (b) 23.5% w.b., for different airflows (m3 s-1 m-2).
For each airflow, these errors represent the values obtained by the model that satisfactorily describes the data obtained by Da Silva et al. (2006). It is observed that the model implemented using ANSYS® program, provides reliable estimates, where all airflows tested have relative errors smaller than 7%.
Table 2 presents the values of the distributed resistances (RD1) of the pulped coffee bed, for various airflows, according to the optimization process and relative errors involved in the optimization. For such values of distributed resistance, the average of 7.2 x 107 m-2 was obtained, considering all the airflows used.
TABLE 2
Distributed resistances (RD1) of the pulped coffee bed for various airflows according to the optimization process and relative errors for various airflows and moisture contents
| Water Content (%) | Airflow (m3s-1m-2) | RD1 (m-2) | Average Relative Error |
|---|
| 12,7 | 1,650E-01 | 7,964E+07 | 1,496E-05 |
| 2,530E-01 | 7,027E+07 | 1,144E-02 |
| 2,630E-01 | 6,785E+07 | 3,190E-03 |
| 23,5 | 1,650E-01 | 7,590E+07 | 1,009E-03 |
| 2,530E-01 | 6,807E+07 | 9,167E-04 |
| 2,630E-01 | 6,785E+07 | 3,190E-03 |
Ergun (1957) provides an expression to determine permeability (which is considered constant) of a packed bed of particles with homogeneous spheres. Thus, it was verified that the permeability, by the Ergun equation, is 4.94 x 10-8 m2, for a diameter of 5.8 mm and a porosity of 42.5%.
Moreover, on the analyzed considerations, the permeability of the bed reached a mean of 1.39 x 10-8 m, where the permeability is inversely proportional to the distributed resistance.
CONCLUSIONSAnalyses of the results obtained in this work allow the following conclusions about the pressure drop across a bed of coffee beans:
By varying the depth in the column, the static pressure increases with higher water content or higher air flow density;
Considering the flow densities and the depths used in the bed, the values obtained by ANSYS software 15.0.1, reliably describe the ones obtained by the model of Da Silva et al. (2006).
The distributed resistances of the coffee bed determined from simulations using the finite element technique have a mean of all fluxes and water contents of 7.16 x 107 m -2, with average relative error of 3.29 x 10-3 m2, showing a tendency to decrease with increasing airflow density.
Ergun equation, used to estimate the resistance offered to the airflow by a column of spherical and homogeneous particles, is not reasonable to predict the resistance of the coffee beds submitted to different flow densities and water contents.
INTRODUÇÃOPara a obtenção de um armazenamento eficiente de grãos agrícolas a granel, o produto deve ser submetido a operações de secagem e de aeração. A execução destes processos prolonga o período de armazenamento e evita a deterioração do produto, resultante da sua atividade biológica. Sendo assim, uma massa de ar é geralmente forçada a passar pelo produto agrícola; o ar, encontrando resistência do produto granular a sua passagem, escoa pelos espaços intergranulares. A determinação da resistência ao fluxo de ar para produtos agrícolas pode ser medida pela queda de pressão, sendo fundamental em projetos de sistemas de secagem e aeração (Brandão et al., 2016; Korese et al., 2016; Olatunde et al., 2016; Gao et al., 2018).
A resistência ao fluxo de ar em sistemas de secagem e aeração depende de diversos fatores como intensidade do fluxo de ar, altura da camada de grãos, presença de impurezas no produto, tamanho, forma, teor de umidade, distribuição dos grãos na massa granular e rugosidade do produto (Brooker et al., 1992).
O método de enchimento da coluna de grãos, a sua compactação e a direção do fluxo de ar, também influenciam na resistência de um produto à passagem de um fluxo de ar. Nesses sistemas, as chapas perfuradas, os dutos perfurados e as tubulações, são responsáveis pelo aumento da queda de pressão (Gratão et al., 2013; Teixeira et al., 2015).
Vários autores como Corrêa et al. (2001) estudaram os efeitos da densidade do fluxo de ar, do tamanho e da quantidade de impurezas, na queda de pressão estática em massas granulares de feijão; além de ajustar os modelos matemáticos empíricos básicos de acordo com os dados obtidos. Outros pesquisadores estudaram a variação da pressão estática ao longo de uma coluna de café, em função da densidade do fluxo de ar, do teor de umidade, da massa específica aparente e da profundidade da camada do produto (Afonso, 1994).
Teoricamente, o problema de escoamento de fluidos é definido pelas leis de conservação de massas, de momentum e de energia. Quando se consideram as seguintes restrições: (a) o fluido é Newtoniano, (b) o fluido é incompressível, (c) não ocorre mudança de fase, (d) o escoamento é isotérmico e permanente, (e) o domínio espacial do problema não muda com o tempo e; (f) a viscosidade do fluido é constante, a equação de Navier-Stokes é dada pela Equação 01.
Assim, a Equação 01 pode ser reescrita em função das componentes x, y e z (Equação 02).
Vários pesquisadores têm determinado experimentalmente a queda de pressão em colunas de produtos agrícolas Iqbal et al. (2015); Dilmac et al. (2016); Du et al. (2016) e Horabik et al. (2016). Enquanto outro tem estudado a expressão do gradiente de pressão em função do fluxo de ar, imposto a uma coluna de grãos (Shedd, 1953; Hukill y Ives, 1955; Haque et al., 1978; Hunter, 1983; Giner y Denisienia, 1996).
Diversas técnicas numéricas têm sido amplamente aproveitadas na resolução de problemas de escoamento de fluidos, dentre as quais a técnica de elementos finitos vem sendo empregada com sucesso pelos pesquisadores para a resolução de diferentes problemas, envolvendo escoamento de ar em produtos agrícolas como por exemplo para a secagem Beigi (2017); Chiang et al. (2017); Lemus-Mondaca et al. (2017) e para a resistência distribuída De Andrade et al. (2001); Khatchatourian e Savicki (2004); Devilla et al. (2005); Yue e Zhang (2014); Moses et al. (2015). Por estas razões, os objetivos gerais do presente trabalho foram primeiramente analisar, através da técnica de elementos finitos, a queda de pressão estática em um leito recheado de café, submetido a diferentes fluxos de ar e teores de água; assim como determinar a permeabilidade do leito aos diferentes fluxos de ar e teores de água.
MÉTODOSLeito de partículas e fluxos de ar: Nas simulações das quedas de pressão no interior de um leito de partículas, utilizou-se a geometria de um duto de seção transversal circular (0,1525 m de raio) com 1,00 m de comprimento, posicionado na vertical. O duto foi recheado com café despolpado (Coffea arabica L.) variedade Catuaí, a teores de água de 12,7 e 23,5% b.u. e os fluxos de ar impostos na entrada do leito foram de 0,165; 0,253 e 0,263 m3 s-1 m-2.
Análise por elementos finitos: A determinação do perfil de pressão e da velocidade em problemas de escoamento de fluidos em dutos sem partículas foi obtida através da técnica de elementos finitos, assessorada por “softwares” interativos para análise de sistemas, o ANSYS® disponível comercialmente.
Os parâmetros de entrada para os programas computacionais desenvolvidos nesta área foram, basicamente: as propriedades do fluido, as condições de contorno em todas as superfícies abertas ou fechadas do sistema e o tipo de análise a ser desenvolvida. Neste sentido, as condições de contorno nas superfícies abertas podem ser velocidades, pressões ou combinações destes parâmetros. Como resultado, têm-se as distribuições de velocidade e de pressão nos nós, provenientes da discretização do sistema.
Neste trabalho, o sistema ANSYS versão 15.0 foi utilizado para o desenvolvimento de um programa-fonte, para realizar uma análise tridimensional do escoamento de ar em uma coluna fixa de grãos de café. O produto no interior da coluna foi considerado equivalente a uma resistência distribuída no interior do duto, ou seja, correspondente aos termos Rx, Ry e Rz, nas Equações (2a-b-c).
Portanto, foi desconsiderada a geometria do meio poroso e modelada como uma resistência distribuída. Como se observa na Equação (03), tal resistência pode ser devido a um, ou a uma combinação dos seguintes fatores: uma perda localizada de pressão (F); um fator de fricção (f) ou um fator (C) relacionado à permeabilidade (K) do meio, tal que (C=1/K). Assim, o gradiente de pressão total, na direção x, pode ser expresso por ANSYS (2013):
O duto foi dividido em 1440 elementos do tipo FLUID142, com oito nós, resultando em 1927 nós ao final da discretização, como é mostrado na Figura 1. As entradas do programa-fonte foram as propriedades do ar (assumidas constantes), o valor de C: mencionado no texto como RD1 (resistência distribuída) e as condições de contorno, que pela estrutura do programa computacional, foram impostas para todas as superfícies abertas ou fechadas que delimitaram o meio sendo investigado.
Malha e condições de contorno para análise por elementos finitos.
Foram usadas como condições de contorno: (1) velocidades nulas (V1), segundo os três eixos coordenados na parede lateral interna do duto; (2) velocidade constante e uniformemente distribuída (V2) na base do duto e; (3) pressão (P3) igual a zero (referência) em todos os nós da extremidade superior do duto.
Comparação dos modelos: Os resultados da queda de pressão do ar escoando através de uma coluna de grãos de café, determinados pela técnica de elementos finitos, foram comparados com aqueles provenientes dos coeficientes das equações quadráticas ajustadas para descrever o comportamento da pressão estática em função do teor de água, profundidade na coluna e densidade do fluxo para o café despolpado sem impurezas (da Silva et al., 2006). Os valores da massa específica real, da massa específica aparente e da porosidade para o café despolpado com teor de água de 12,7 % foram de 0,7929 g cm-3, 0,3879 g cm-3 e 51,59 % respectivamente. Enquanto que as mesmas propriedades físicas para as amostras com 23,5 % foram de 0,8685 g cm-3, 0,4635 g cm-3 e 48,35 % respectivamente (Tabela 1). A validade do modelo proposto pelos autores são para as profundidades que variam entre 0,00 e 0,95 m e para fluxos entre 0,16 e 0,26 m3 s-1 m-2.
TABELA 1
| Coeficientes | a | b | c | d | e | f | g | h | i | j |
|---|
| -1,31 | 0 | 95,71 | 27,63 | -651,14 | 1.202,38 | 6,62 | 1.355,89 | -1,26 | 83,23 |
RESULTADOS E DISCUSSÃONa Figura 2 é apresentado o ¨contour plot¨ das pressões estáticas simuladas pelo ANSYS da amostra de café com 12,7 % de teor de água, sem impureza e com fluxo de ar de 0,165 m3 s-1 m-2. Pode-se observar que ao longo da coluna, a partir do eixo das coordenadas (X, Y, Z), os valores obtidos decrescem. De acordo com dados simulados, a pressão máxima e mínima na coluna se localizam respectivamente no eixo das coordenadas e no topo da coluna, sendo de 374,9 Pa e 0 Pa.
Solução nodal do café despolpado com teor de água em 12,7 % b.u. e fluxo de ar em 0,165 m3 s-1 m-2.
Os resultados das simulações das variações de pressão em diferentes profundidades de uma coluna de café despolpado com teor de água em 12,7 % b.u. para diferentes fluxos de ar são apresentados na Figura 3(a), e para amostras com teor de água em 23,5 % b.u. na Figura 3(b).
Queda de pressão em função da profundidade em uma coluna de café despolpado com teores de água de (a) 12,7 % b.u.e (b) 23,5 % b.u., para fluxos de ar (m3 s-1 m-2).
Pôde-se observar que a densidade do fluxo de ar possui relação direta com a resistência do escoamento do ar, bem como com a profundidade na coluna de café. Como esperado, os valores de pressão estática crescem com o aumento da densidade do fluxo de ar aplicada na massa. Por outro lado, não se observa diferença de pressão estática entre os tratamentos com diferentes teores de água do café despolpado analisados.
Os erros relativos percentuais correspondentes às quedas de pressões obtidas pela simulação são apresentados na Figura 4(a) para amostras com teor de água de 12,7 % e na Figura 4(b) para amostras com teor de água de 23,5 %. Nesta figura observa-se que os valores dos erros relativos diminuem a medida em que se aumenta a camada do produto, o que está em concordância com os dados obtidos por Moses et al. (2014a, 2014b, 2014c).
Erros relativos envolvidos nos valores simulados para a queda de pressão nas profundidades da coluna de café despolpado com teores de água de (a) 12,7 % b.u. e (b) 23,5 % b.u, para fluxos de ar (m3 s-1 m-2).
Para cada fluxo de ar, os erros representam os valores obtidos pelo modelo que satisfatoriamente descreve os dados de Da Silva et al. (2006). Aliás, observa-se que o modelo implementado usando o programa ANSYS® proporciona estimativas confiáveis, onde todos os fluxos de ar testados apresentam erros relativos inferiores a 7 %.
Os valores das resistências distribuídas (RD1) representativas do leito de café despolpado, para cada valor de fluxo de ar provenientes do processo de otimização e acompanhados dos erros relativos envolvidos na otimização, são apresentados na Tabela 2. Para tais valores de resistência distribuída, obteve-se a média de 7,2 x 107 m-2, considerando-se todos os fluxos de ar empregados.
TABELA 2
Valores da resistência distribuída (RD1) da coluna de café despolpado, acompanhados dos erros relativos médios, para diferentes fluxos de ar e teores de água
| Teor de água (%) | Fluxo de ar (m3s-1m-2) | RD1 (m-2) | Erro Relativo Médio |
|---|
| 12,7 | 1,650E-01 | 7,964E+07 | 1,496E-05 |
| 2,530E-01 | 7,027E+07 | 1,144E-02 |
| 2,630E-01 | 6,785E+07 | 3,190E-03 |
| 23,5 | 1,650E-01 | 7,590E+07 | 1,009E-03 |
| 2,530E-01 | 6,807E+07 | 9,167E-04 |
| 2,630E-01 | 6,785E+07 | 3,190E-03 |
A pesquisa desenvolvida por Ergun (1952), fornece uma expressão para a determinação da permeabilidade a qual é considerada constante em um leito recheado de partículas com esferas homogêneas. Assim, no presente trabalho foi verificado que a permeabilidade pela equação de Ergun é de 4,94 x 10-8 m2, para um diâmetro de 5,8 mm e porosidade de 42,5 %. Sobre as considerações analisadas, a permeabilidade do leito obteve uma média de 1,39 x 10-8 m, onde a permeabilidade é inversamente proporcional a resistência distribuída.
CONCLUSÕESAo variar a profundidade na coluna, os valores de pressão estática se tornaram maiores a medida em que se empregou maior teor de água ou maior densidade de fluxo de ar.
Com as densidades de fluxo utilizadas e com as profundidades na coluna, os valores obtidos pelo software ANSYS 15.0.1 descreveram de maneira confiável os valores obtidos pelo modelo de Da Silva et al. (2006).
Os valores de resistência distribuída do leito de café, determinada a partir de simulações e utilizando-se a técnica de elementos finitos, teve uma média entre todos os fluxos e teores de água estudados de 7,16 x 107 m-2, com erro relativo médio de 3,29 x 10-3 m2, apresentando tendência de diminuir com o aumento da densidade do fluxo de ar.
A equação de Ergun, usada para estimar a resistência oferecida ao fluxo de ar por uma coluna de partículas esféricas e homogêneas, não foi razoável para predizer a resistência dos leitos de café submetidos a diferentes densidades de fluxo e com diferentes teores de água.