Introducción
Los emisores son los elementos más importantes de un sistema de microirrigación y su función principal es permitir la salida del agua a un caudal controlado y en lugares del cultivo previamente determinados según Solomon (1985). Un emisor es un disipador de presión construido especialmente para generar una pérdida de carga localizada induciendo vorticidad, fricción hidráulica o una combinación de las dos (Feng y Wu, 1990).
Los emisores deben proporcionar un caudal bajo, con el objetivo de que los diámetros de las tuberías sobre todo laterales y distribuidoras, sean reducidos; las grandes longitudes que de estas tuberías se emplean en los sistemas de microirrigación hacen que un ligero incremento en su diámetro encarezca de forma importante el proyecto del sistema (Sammis y Wu, 1985). Por otra parte, la presión de servicio de los emisores no debe ser muy baja para minimizar el efecto que sobre la uniformidad del riego tienen los desniveles del terreno y las pérdidas de carga a lo largo de las distribuidoras y los laterales (Vélez-Sánchez et al., 2013). Su diámetro de paso ha de ser lo mayor posible para evitar las obturaciones que es el principal problema en el manejo de los sistemas de microirrigación (Pereira et al., 2010). El objetivo del trabajo es evaluar emisores autocompensantes y no compensantes en sistemas de microirrigación.
Métodos
La investigación se realizó en áreas de la UBPC el Tezón de la Empresa Agroindustrial de Ceballos, en el cultivo de la guayaba con un suelo Ferralítico Rojo Típico. La metodología utilizada para la evaluación de los emisores tipo gotero fue la establecida en la Norma Internacional ISO 9260: 1991 titulada Equipos de Riego para la Agricultura Goteros- Especificaciones y métodos de prueba. Los emisores seleccionados para el estudio fueron los que se encuentran en los sistemas de riego de la UBPC el Tezón.
Para la determinación de la curva caudal- presión q=f (h) se tuvo en cuenta los aspectos señalados en la por la Norma ISO 9260: 1991. Luego se tomaron 4 mediciones de caudal para cada gotero de esta serie (los números 3, 12, 13, 23) seleccionados al azar según Pizarro (1987), y se les determinó la variación del caudal de emisión en función de la presión de entrada. Se evaluó cada emisor por etapas y con presiones no mayores a 50 kPa desde la presión cero hasta 1,2 veces la presión máxima (Pmax). Los emisores regulados fueron probados a distintas presiones dentro del rango de regulación. La lectura de los resultados se tomó durante 3 minutos después de alcanzar la presión de prueba.
La determinación de la variación del caudal producto de la temperatura del agua se llevó a cabo midiendo tres veces la descarga de cada uno de los emisores seleccionados al azar con los números siguientes (3, 12,13 y 23) de los 25 emisores evaluados de cada modelo según Pizarro (1987), a distintas temperaturas del agua en un rango de 7 - 55oC a la presión nominal de cada gotero y la mitad del intervalo de regulación para los goteros autocompensados. La temperatura del agua fue medida con termómetros en la fuente de abasto de agua y en la entrada del lateral. La diferencia de temperatura entre estas lecturas, no debió exceder los 20C.
Resultados y Discusión
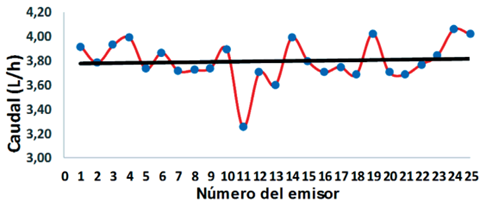
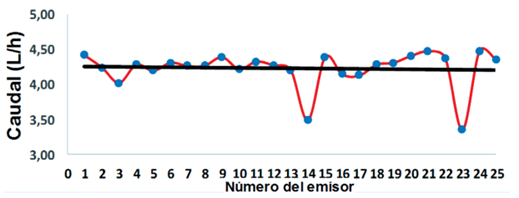
En las Figuras 1, 2 y 3 se presentan los resultados obtenidos en la distribución del caudal de los emisores estudiados. En el caso del gotero Vip Line la mayor dispersión se obtuvo en el emisor número 11, ocurriendo un descenso del caudal hasta unos 3,4 L/h, el gotero O-Tiff no compensante manifestó las mayores variaciones de caudales en los emisores (9, 13, 19 y 21) Como puede observarse en las mismas, en el emisor Naan PC la mayor dispersión de caudales se obtuvo, esencialmente en los goteros números 14 y 23 de la tubería lateral de prueba, en los cuales el caudal descendió casi a unos 3 L/h.
Figura 1. Variación del caudal del gotero modelo Vip Line autocompensante con caudal nominal de 3.9 L/h.
Figura 2. Variación del caudal del gotero Naan PC modelo autocompensante con caudal nominal de 3.8 L/h.
Los resultados obtenidos en esta investigación coinciden con los informados por Solomon (1985), este autor obtuvo que el caudal de los emisores de acuerdo con las especificaciones del fabricante, sufran al colocarlo en el campo una serie de variaciones, unas inherentes al propio emisor y otras a las condiciones a las que trabaja. Carmenates et al. (2014), obtuvieron resultados diferentes con emisores de un mismo modelo y aparentemente idénticos, pero con ligeras diferencia constructivas. Lo anterior se justifica teniendo en cuenta lo planteado por Benami y Ofen (1984), este autor refiere que todo proceso industrial es imperfecto, por tanto, el producto elaborado experimenta variaciones dentro de una tolerancia aceptable y siempre existirá una ligera diferencia entre objetos que aparentemente resultan idénticos.
Las variaciones de caudales en los emisores evaluados también pueden estar dadas a que los emisores experimentan un envejecimiento acelerado debido a la diferencia de temperatura a que se someten durante el día y la noche. Los elastómeros de los goteros autocompensantes se ven particularmente afectados por este fenómeno, coincidiendo con los resultados reportados por Bucks y Myers (1973).
Resultados de la determinación de la curva caudal-presión (q=f (h))
En las Figuras 4, 5 y 6 se muestran cómo varía el caudal en función de la presión en los emisores estudiados cuando son sometidos a distintas presiones.
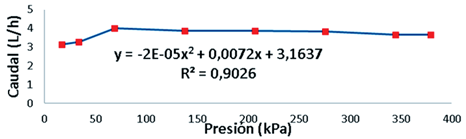
En la Figura 4 se presenta la relación caudal presión del emisor Vip Line con flujo autocompensante, caudal nominal de 3,9 L/h y un rango de compensación entre (68-413 kPa), el cual responde a una ecuación obtenida en condiciones experimentales de tipo polinómica en sentido ascendente. Es necesario destacar, que la relación entre el caudal y la presión resultó típica de la condición de autocompensación propia de los emisores de este tipo. Puede observarse la tendencia al paralelismo de la curva q= f(h) respecto al eje de las presiones específicamente en el intervalo comprendido entre 75 kPa y 375 kPa, indicando que el comportamiento de autocompensación del caudal con respecto a la presión aplicada manifestó una relación satisfactoria con un coeficiente de determinación del 90% (R2= 0,9026).
Estos resultados coinciden con los obtenidos por (López et al., 2009; Hernández et al., 2010; Pereira et al., 2010; El-Nemr, 2012) con otros modelos de emisores, donde evalúan goteros compensantes y no compensantes determinando el régimen de flujo para cada modelo evaluado.
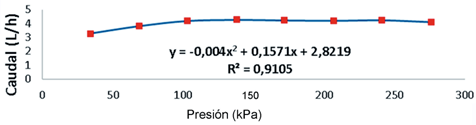
En la Figura 5 se muestran los resultados obtenidos en la relación caudal emitido presión de servicio (q= f (h)) del gotero Naan PC, con un caudal nominal de 3,8 L/h y un rango de compensación de 68- 475 kPa.
Por el comportamiento de la curva q= f (q) obtenida se infiere que el caudal responde a las presiones de servicio siguiendo determinada tendencia de compensación de acuerdo al valor obtenido del coeficiente de determinación del 91%. R2=0,9234.
Sin embargo, se evidencia que el caudal aumenta en una proporción muy baja respecto al incremento de la presión, demostrando así, la alta compensación de este gotero, lo cual se evidencia por el hecho de que a 100 kPa el caudal alcanzó los 4,2 L/h y a 275 kPa el caudal resultó de 4,0 L/h existiendo una alta capacidad de compensación en este modelo. Los resultados coinciden con los obtenidos por Al-Ghobari (2012).
En los emisores evaluados el comportamiento de la curva caudal presión se refleja en una ecuación de tipo polinómica y= ax2 + bx + c obtenida experimentalmente, ya que fue esta con la que mejor ajuste se obtuvo con coeficientes de determinación con valores superiores al 90% en todos los casos. Los resultados coinciden con los obtenidos por Carmenates et al. (2012).
Figura 5. Relación caudal-presión del gotero Naan PC modelo autocompensante con caudal nominal de 3,8 L/h
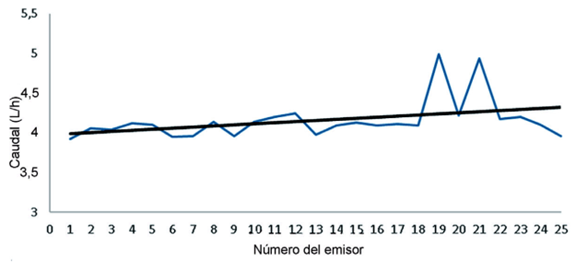
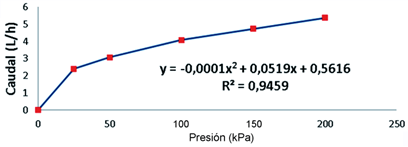
La Figura 6 muestra los resultados de la relación caudal presión del gotero O-Tiff con flujo no compensado, presión nominal 100 kPa y caudal nominal de 4 L/h.
Como puede observarse en la citada figura la ecuación de mejor ajuste con valores del coeficiente de determinación del 94%. R2=0.9459 es de tipo polinómica, lo cual evidencia una fuerte relación entre el caudal emitido y la presión de servicio, es decir, al contrario de los emisores autocompensantes, para cada incremento de la presión corresponde un incremento del caudal. A 50 kPa se obtuvo un caudal de 3 L/h y a 100 kPa el caudal resultó de 4 L/h y a 200 kPa el caudal fue de 5,3L/h, estos emisores por lo anteriormente explicado resultan de más mala calidad y por tanto su precio en el mercado resulta más bajo.
Resultados relación caudal-temperatura del agua (q=f(T)) de emisores
Los resultados experimentales obtenidos de la variación del caudal, de los emisores estudiados, sometidos a distintas temperaturas, responden a una ecuación lineal de la forma siguiente:
Puede observarse que se obtuvieron ecuaciones experimentales con coeficientes de determinación por encima del 90% para todos los modelos de goteros evaluados. Los resultados obtenidos se corresponden con los reportados por Loboa et al., (2011).
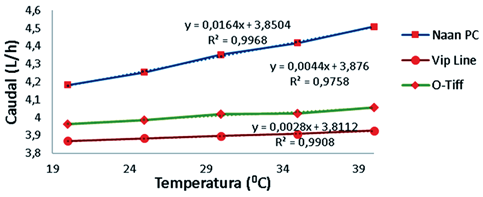
En la Figura 7 se presentan los resultados obtenidos en los ensayos realizados en la tubería lateral de prueba de las variaciones de caudal de emisores tipo goteros modelos Naan PC, Vip-Line autocompensantes y O-Tiff no autocompensante al ser sometidos a distintas temperaturas del agua.
Los resultados experimentales obtenidos de la variación del caudal de los emisores estudiados sometidos a distintas temperaturas, indican que presentan la tendencia de responder a una ecuación lineal. Puede observarse que se obtuvieron ecuaciones experimentales con coeficientes de determinación por encima del 90% para todos los modelos de goteros evaluados. Los resultados obtenidos coinciden con los obtenidos por Goyal (2013) y Valipour (2014). El emisor modelo Naan PC fue el que presentó mayor variación del caudal producto de la temperatura del agua alcanzando valores superiores a los 390C, estos incrementos de la temperatura están dados a que se colocó un calentador comercial en la tubería lateral de prueba en condiciones experimentales.
Sin embargo, Pizarro (1987) y Ouazaa et al. (2013), obtuvieron con otros modelos de emisores compensantes que el aumento de la temperatura disminuye la viscosidad cinemática del agua y aumenta el número de Reynolds. En consecuencia disminuye el coeficiente de Darcy- Weisbach y aumenta el caudal del emisor.
Figura 7. Determinación de la curva caudal temperatura del agua de los goteros autocompensantes y no compensantes.
La sensibilidad del caudal a la temperatura del agua se expresa por medio de la pendiente de la curva (n), presentando los valores más bajos en los modelos Vip Line y O-Tiff y un valor relativamente alto en Naan PC. Esto tiene su explicación en que la sección de paso del agua en los goteros autocompensantes es de régimen turbulento, por lo tanto, el caudal no se ve afectado por la viscosidad del agua, la que varía a distintas temperaturas. Además se puede observar que el coeficiente de relación es alto para los tres emisores evaluados, para el caso del Naan PC (R2= 0,9968); O-Tiff (R2= 0,9758) y el Vip Line (R2= 0,9908). Los resultados coinciden con los obtenidos por Vélez-Sánchez et al. (2013) y Rodríguez et al. (2014), para emisores con similares características hidráulicas y mecánicas pero con coeficientes de determinación más bajos que los obtenidos en este trabajo.
Conclusiones
Las características hidráulicas y mecánicas de los emisores evaluados conformadas básicamente por la curva caudal-presión, y la relación caudal-temperatura constituyen parámetros fundamentales para poder realizar un adecuado diseño y manejo de los sistemas de microirrigación. Obteniéndose para el comportamiento de la curva caudal-presión una ecuación de tipo polinómica y= ax 2 + bx + c obtenida experimentalmente para los modelos de emisores evaluados con un ajuste del coeficiente de relación con valores superiores a 0,90 para ambos casos.
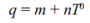 (
(