INTRODUCCIÓN
El neumático une la superficie del suelo con el vehículo y confiere a los vehículos adherencia, estabilidad, confort y es responsable de gran parte de la energía que se consume. Los mismos se clasifican en convencionales o diagonales y los radiales. Debido a la poca resistencia de los neumáticos radiales a cargas de impacto laterales, en equipos pesados y máquinas agrícolas aún se emplean neumáticos convencionales dependiendo del desempeño del equipo. Las máquinas agrícolas se desplazan por terrenos no pavimentados, terraplenes, preparados para sembrar y sin preparar, los cuales poseen condiciones muy adversas, por lo que el estudio de las condiciones del neumático adquiere mayor importancia. De esta forma queda evidenciada la necesidad de contar con diseños de neumáticos que garanticen la eficiencia y el buen funcionamiento de los remolques agrícolas.
En el diseño de neumáticos se han empleado métodos llenos de simplificaciones e idealizaciones, que abordan de una forma sencilla y básica el problema, por lo que no permiten obtener con exactitud su comportamiento estático ni dinámico, ni aportan datos precisos de desplazamientos, masa, volumen o distribución espacial. Con los métodos numéricos, es posible obtener modelos de simulación numérica con un alto grado de precisión y fiabilidad (Singh y Singh, 2015; Wan et al., 2016; Castro y Güiza, 2017). El comportamiento mecánico de los neumáticos ha sido estudiado y modelado por varios investigadores como: Kabe y Koishi (2000); Bolarinwa y Olatunbosun (2004); Senatore y Sandu (2011); Stickle et al. (2011); Dalmau et al. (2014); Lee y Gard (2014) . Recientemente se encuentran estudios como el realizado por González et al. (2012); Taheri et al. (2015), donde exponen métodos de caracterización de suelo, neumáticos y la interacción entre ellos. Lee (2015), evalúa un modelo estocástico para el efecto de la interacción entre el suelo y el neumático considerando el deslizamiento combinado con resultados aceptables. Zhao et al. (2015), realizaron un modelo por el método de los elementos finitos (MEF) de una rueda elástica mecánica, coincidiendo este con los resultados que obtuvieron de forma experimental.
El método de los elementos finitos, como método numérico de discretización asistido por computadora, constituye una vía alternativa al método analítico de análisis del medio continuo, que facilita la solución de problemas complejos de ingeniería, siendo considerado una herramienta de indudable valor práctico y de gran aplicación a nivel mundial
En el MEF, un dominio dado se divide en subdominios llamados elementos finitos y se desarrolla una solución aproximada para cada uno de los subdominios. El complejo sistema de puntos llamados nodos que emplea el MEF hace una red llamada malla (Lozada y Suquillo, 2018). Esta malla está programada para contener el material y las propiedades de la estructura que definen como esta reaccionará ante ciertas condiciones de carga. A los nodos se les asigna una densidad por todo el material dependiendo del nivel de tensiones anticipado en un área. La malla actúa como la red de una araña en la que desde cada nodo se extiende un elemento de malla adyacente. Este tipo de red vectorial es la que lleva las propiedades del material al objeto, creando varios elementos.
El objetivo del presente trabajo fue obtener un modelo numérico de simulación para el neumático (7.50-20), que logre explicar de forma eficaz el comportamiento de las deflexiones estáticas a diferentes presiones de inflado. El desarrollo de este modelo beneficiará de gran manera el diseño de neumáticos dando una visión general de la relación entre aspectos como la presión de inflado, la carga y la deflexión.
MÉTODOS
Descripción del sistema objeto de investigación
Para la investigación se emplea un neumático diagonal de tipo 7.50-20, en la Figura 1 se describe el sistema llanta-neumático donde sus dimensiones generales sin cargas actuantes son, anchura y altura de la sección, diámetro y radio del neumático sin carga y el diámetro de la llanta, los valores de sus dimensiones aparecen reflejadas en la Tabla 1.
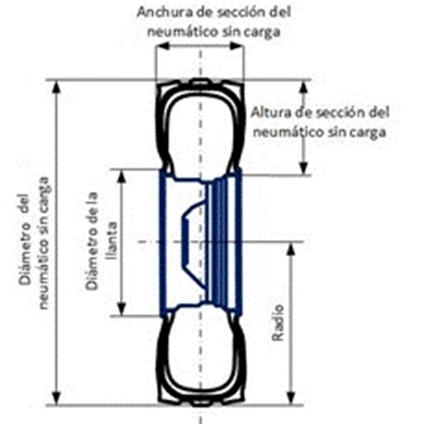
Fig. 1.
Dimensiones generales del sistema llanta-neumático.
Tabla 1.
Valor de las dimensiones generales del sistema llanta-neumático
|
| Anchura de sección | Altura de sección | Diámetro de llanta | Diámetro del neumático sin carga | Radio del neumático sin carga |
|---|---|---|---|---|---|
| Pulgadas | 7,50 | 9 | 20 | 38 | 19 |
| mm | 190,5 | 228,5 | 508 | 965 | 482,5 |
Para el correcto desarrollo del MEF existen pasos que deben de cumplirse dependiendo del caso de análisis, los cuales son: 1. Digitalización del sistema objeto de estudio con herramientas de diseño asistido por computadora (CAD); 2. Importar hacia el programa de análisis por el método de los elementos finitos la geometría digitalizada; 3. Seleccionar el tipo de estudio; 4. Aplicar las propiedades del material; 5. Definir las condiciones de frontera del sistema; 6. Aplicar contactos entre componentes; 7. Realizar análisis de convergencia; 8. Crear mallado según los resultados del análisis de convergencia.
Desarrollo de la simulación numérica del sistema llanta-neumático por MEF
Se emplearon dos modelos geométricos los cuales fueron simulados bajo diferentes condiciones de trabajo.
El modelo uno para el sistema llanta-neumático se confeccionó a partir de un esbozo detallado de la sección del neumático empleando el software Solid Works 2012, las partes componentes del modelo uno aparece en la Figura 2.

Fig. 2.
Elementos componentes del modelo uno para el neumático 7.50-20. 1. Capa exterior del neumático (Bandas laterales y de rodadura); 2. Capa interior del neumático compuesto por cuerdas y caucho; 3. Llanta metálica y 4. Superficie rígida de apoyo.
En este caso se consideró la diferencia en la composición de los materiales de su geometría (zona de rodaje y banda lateral), a los cuales se les asigna valores del módulo de elasticidad y del coeficiente de Poisson diferentes. Este modelo es procesado empleando el software de análisis por elementos finitos ANSYS R15.0. Mediante el programa Autodesk Inventor 9.0 se desarrolló el modelo dos, el cual difiere de la geometría del modelo uno en la cantidad de componentes empleados en su modelación. Para este caso se combinaron la capa exterior e interior formando un solo elemento. El modelo dos es una simplificación que mantiene la geometría original, pero no se consideran diferencias en el módulo de elasticidad de las diferentes partes del mismo, aplicándose un módulo de elasticidad y coeficiente de Poisson global. El análisis del modelo se realiza por el método de los elementos finitos con el programa Cosmos DesignStar 3.0.
Condiciones de frontera
Para el estudio de los dos modelos de neumáticos se consideraron tres niveles de presión de inflado 0,13 MPa baja presión de inflado, 0,23 MPa condición normal y 0,31 MPa para una situación de exceso de presión en el neumático. A cada una de las condiciones de presión de inflado se le aplicaron cargas estáticas verticales en el centro de la rueda en el semi-arco inferior del agujero de la llanta que van desde 3 300 hasta 6 800 N a intervalos de 500 N. A la zona de contacto del neumático con la plancha metálica se le aplicaron restricciones fijas, se restringió el movimiento horizontal por lo que excesivamente se trabaja en el eje vertical. El resto de las uniones del modelo se consideraron soldadas (Figura 3).
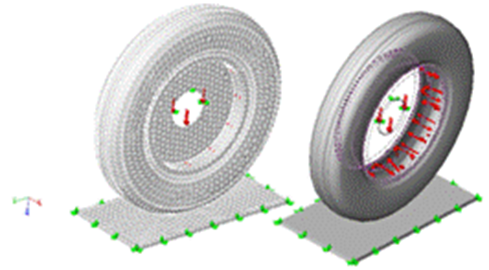
Fig. 3.
Condiciones de frontera de los modelos de simulación por el método de los elementos finitos.
Los datos del módulo de elasticidad del modelo uno en sus diferentes elementos fueron tomados de estudios de Flores et al. (2010), para el caso del modelo dos se aplicó un módulo de elasticidad global, calibrado en función de los resultados experimentales. Las propiedades físico mecánicas de los materiales empleados en la simulación de ambos modelos aparecen en la Tabla 2. Las características de la malla empleada ambos modelos se muestran en la Tabla 3.
Tabla 2.
Partes componentes de los modelos y sus propiedades físico mecánicas
Tabla 3.
Características de la malla empelada en la simulación
Ensayos experimentales
En correspondencia con los resultados de los modelos numéricos de simulación, se desarrollaron las investigaciones, observaciones y mediciones experimentales. Para cada nivel de presión de inflado se aplicaron cargas estáticas de manera ascendente y descendente, con tres repeticiones por cada ensayo experimental. La instalación experimental está compuesta por un remolque agrícola de una carga máxima de dos toneladas y un solo eje de ruedas, el cual fue modificado para los experimentos (Figura 4). Para medir el valor de la carga aplicada se empleó una celda de carga a compresión modelo CLY, marca CRITM, colocado en la parte inferior del neumático y un amplificador con precisión de lectura 10 N ambos dispositivos se muestran en la figura 5 A.
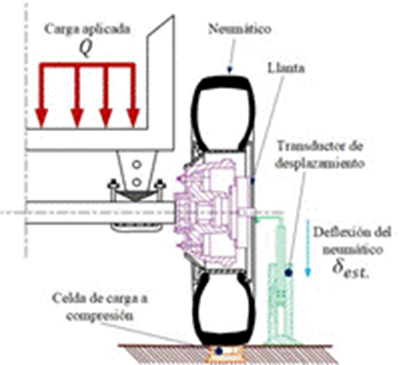
Fig. 4.
Diagrama del ensayo experimental para la determinación de las deflexiones.
Para determinar experimentalmente la deflexión estática ( ) del sistema llanta-neumático, en función de la carga aplicada, se empleó un transductor de desplazamiento marca Kyowa de una precisión de lectura de 0,01 mm (Figura 5 C). El transductor de desplazamiento fue ajustado a cero a partir de la carga representada por el peso propio del remolque sobre el neumático objeto de estudio, que medido a través de la celda de carga resultó de 3,300 N con una deflexión inicial que dependió del nivel de presión de inflado. El voltaje de salida del transductor de desplazamiento era manipulado a través de una caja de cómputo y balance de resistencia modelo SS-24R (Figura 5 B), para luego ser amplificado mediante un amplificador tensométrico modelo SM60D (Figura 5 E), cuyos datos aparecen en la Tabla 4. La presión de inflado de los neumáticos fue ajustada con un manómetro con exactitud de 0,01 MPa (Figura 5 D).

Fig. 5.
Intrumentación de los ensayos experimentales. A) Celda de carga a compresión, B) Caja de cómputo y balance de resistencia, C) transductor de desplazamiento, D) Manómetro y E) Amplificador tensométrico.
Tabla 4.
Datos técnicos del amplificador extensométrico empleado en las mediciones experimentales
Procesamiento y evaluación estadística de los datos primarios
En los casos reales, los ajustes absolutos del modelo a la realidad no se dan. Es por eso que existen una medida que describe como se precisa la predicción de Y en función de X o, al revés, lo inexacta que puede ser la predicción. Se emplea el análisis de regresión lineal para medir la dispersión alrededor de la línea de regresión en cada uno de los estudios por independiente, tanto para los obtenidos de forma experimental como mediante simulación numérica en ambos modelos y considerando los diferentes niveles de cargas y las tres presiones de inflado, permitiendo obtener las ecuaciones de regresión lineal. La comparación entre análisis de regresión y sus ecuaciones permitieron comparar los estudios de simulación numérica con el caso real (experimental). Los datos experimentales se grafican y se les determinan las ecuaciones de regresión: deflexión estática contra carga (Q) y carga contra deformación unitaria estática, para cada presión de inflado del neumático.
Cálculo de los errores experimentales
Se realizó un analice de los errores obtenidos en el estudio experimental para cada una de las cargas analizadas, se obtuvieron los errores de regresión, los errores de cargas contra deflexión y los errores aleatorios totales expresados en mm y en porcentaje a escala total.
Para cada variable dependiente en función de la carga (Q), el error total se calculó por:
Eγ
- Error de regresión;
EAtotal- Error aleatorio tota;
Eprop- Error propagación de la variable independiente en la dependiente.
Cada una de ellas se calcula mediante:
tρ, γ
- distribución t de Student para una probabilidad , y un grado de libertad de la ecuación de regresión;
γ = [N - (m+1)]- donde: - número de corridas experimentales, - exponente de la ecuación de regresión;
σr- desviación estándar de regresión
Ykr
- cada valor de la variable dependiente obtenida por la ecuación de regresión para cada valor medido de la variable independiente;
Ykmedida- cada valor medido de la variable dependiente.
Ey-aleatorio
- es el error de lectura del instrumento de medición para la variable dependiente, determinado por:
σy-máx
- desviación estándar máxima del valor medio de la variable dependiente;
tρ, γ- distribución t de Student para una probabilidad ρ = 95 % y grado de libertad γ = n, número de repeticiones en cada corrida o experimento de la variable dependiente; según Muller et al. (1982).
Ey-lectura- error de lectura del instrumento de medición para la variable dependiente.
Se calcula EAtotal para la variable independiente de la forma siguiente:
El error de lectura del instrumento de medición para la variable independiente se determina de la misma forma que para la variable dependiente:
El error de propagación se determina como:
- derivadas parciales de la ecuación de regresión en función de las variables independientes;
Ex-lectura- error de lectura del instrumento de medición para la variable independiente.
ANÁLISIS DE LOS RESULTADOS
Resultados de la medición experimental de la deflexión estática
En la Figura 6 se muestra los resultados de las deflexiones del sistema llanta-neumático, obtenidas experimentalmente para los diferentes niveles de carga y las tres presiones de inflado estudiadas. Se realizó un análisis estadístico que permitió obtener las ecuaciones de regresión lineal para las deflexiones según las tres presiones de inflado experimentadas. Se obtienen altos coeficientes de correlación, superando el estadígrafo R2 el valor de 0,99 en los tres casos. Para la presión de inflado de 0,13 MPa se pudo apreciar que el coeficiente de determinación alcanzo un valor de 0,999 siendo el más alto obtenido. En el caso que el neumático se inflo a presiones de 0,23 MPa se alcanzó un R2 de 0,9947, siendo inferior al valor obtenido para una presión de inflado de 0,31 MPa que fue de 0,9979. Los datos de forma general se ajustan a un comportamiento lineal casi perfecto con pequeñas desviaciones, por lo que es casi proporcional, a iguales incrementos de carga estática se notan similares incrementos de deflexión (Figura 6). También se notó que a medida que aumenta la presión de inflado las deflexiones son menores, esto se debe a que aumenta el coeficiente de rigidez radial del neumático. La pendiente de la recta es menor a mayor presión de inflado su relación inversamente proporcional está dada a que con una mayor rigidez del neumático es preciso valores mayores de carga para obtener las mismas deflexiones.
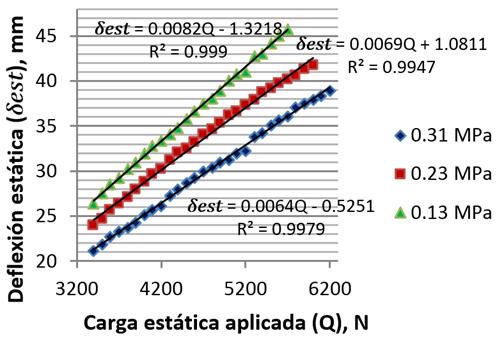
Fig. 6.
Resultados de las deflexiones totales obtenidas de forma experimental para las tres presiones de inflado analizadas.
En la Tabla 5 se muestran los componentes del error total obtenido para cada una de las presiones de inflado, obteniéndose los porcientos de errores relativos a escala total entre 0,89 y 6,37%. Los errores de medición más altos se alcanzaron para el caso donde se trabajó con una presión de inflado de 0,31 MPa, donde el error total fue de 0,88 mm.
Tabla 5.
Errores experimentales
Resultados de la simulación numérica en la determinación de las deflexiones estáticas para el modelo uno
En la Figura 7 A se ve una vista parcial de la salida gráfica del programa de análisis por elementos finitos (ANSYS R15.0) en la simulación numérica del modelo uno para la determinación de las deflexiones estáticas. La Figura 7 B muestra de forma gráfica los resultados de las deflexiones estáticas obtenidas mediante la simulación por el método de los elementos finitos para el modelo uno, donde se aprecia una influencia de la presión de inflado sobre la deflexión estática contraria a los resultados experimentales. Los resultados obtenidos del modelo indican una disminución de los valores de la deflexión estática cuando la presión de inflado es menor, lo cual tampoco concuerda con la experiencia práctica. Por otro lado, si se comparan los valores de las deflexiones obtenidos con el modelo uno para las diferentes cargas, con los obtenidos experimentalmente se aprecia que estos últimos superan entre 3 y 4 veces a los primeros. Estos resultados pueden estar ocasionados fundamentalmente, por no contar con los datos específicos sobre las propiedades mecánicas (fundamentalmente el módulo de elasticidad) de las partes componentes del neumático, los cuales han sido tomados de trabajos anteriores realizados sobre otros tipos de neumáticos. Por otro lado, el comportamiento del modelo uno estudiado mediante un análisis de regresión muestra una pendiente de 0,0011 para las tres presiones de inflado estudiadas.
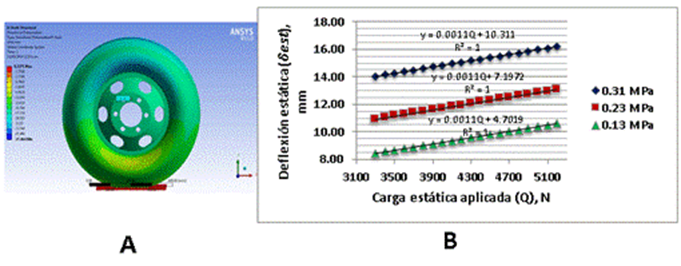
Fig. 7.
Estudios efectuados con el modelo uno. A) Salida gráfica del programa ANSYS R15.0 en la determinación de las deflexiones estáticas. B) Regresión entre la carga aplicada y las deflexiones estáticas obtenidas en el modelo uno para diferentes niveles de inflado.
Resultados de la simulación numérica en la determinación de las deflexiones estáticas para el modelo dos
En la Figura 8 A se ve una vista parcial de la salida gráfica del programa de análisis por elementos finitos (Cosmos DesignStar 3.0) en la simulación numérica del modelo dos. El procesamiento estadístico de estos resultados arrojó las ecuaciones de regresión que se exponen en la Figura 8 B, donde se aprecia una alta coincidencia entre los resultados obtenidos con el modelo dos de elementos finitos y los resultados experimentales expuestos en la Figura 6. Comparando los resultados obtenidos a presiones medias de inflado (0,23 MPa) y con una carga aplicada estáticamente de 4 800 N, se obtienen valores de la deflexión de 34,49 mm y 34,70 mm para el modelo dos y el experimento respectivamente, lo que representa una desviación relativa de sólo un 0,06 %. Al comparar las pendientes de regresión obtenidas por ambos métodos se aprecia que para el caso experimental que fue de 0,0082 para una presión de inflado de 0,13 MPa, en el caso que se analizó la presión de 0,23 MPa la pendiente alcanzo un valor de 0,0069 y en la máxima presión de inflado (0,31 MPa) el valor fue de 0,0064. Para el caso del modelo dos la pendiente alcanzo 0,0077; 0,0076 y 0,0076 para las presiones de 0,13; 0,23 y 0,31 MPa respectivamente, demostrando que poseen valores muy cercanos. Asimismo, el resultado obtenido para diferentes niveles de inflado del neumático en el caso del modelo dos, refleja un incremento de la deflexión cuando disminuye la presión de inflado, lo que coincide con los resultados experimentales.
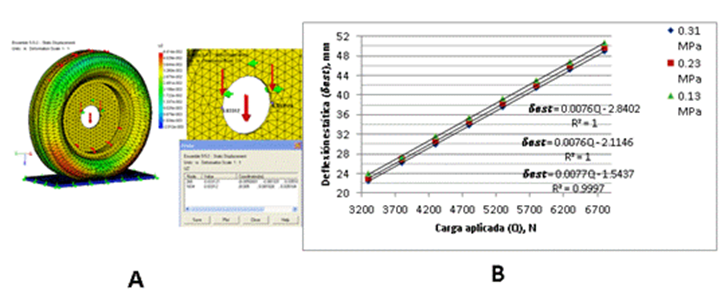
Fig. 8.
Estudios efectuados con el modelo dos. A) Salida gráfica del programa Cosmos DesignStar 3.0 en la determinación de las deflexiones estáticas. B) Regresión entre la carga aplicada y las deflexiones obtenidas en el modelo dos para diferentes niveles de inflado.
CONCLUSIONES
El análisis de regresión arrojó una pendiente de 0,0082 para una presión de inflado de 0,13 MPa, 0.0069 para una presión de 0,23 MPa y de 0,0064 en la máxima presión de inflado (0,31 MPa).
Para el caso del modelo uno de simulación numérica por el método de los elementos finitos se aprecia una relación directa entre la presión de inflado y la deflexión estática, detectándose las mayores deflexiones con la mayor presión de inflado, resultados que contradicen las pruebas experimentales.
La desviación relativa de las deflexiones obtenidos entre el modelo dos y los resultados experimentales para niveles medios de carga (4 800 N) y presión de inflado de 0,23 MPa, fueron de sólo un 0,06 %. Mediante la simulación numérica por el método de elementos finitos es posible determinar la deflexión producida en el sistema llanta-neumático 7.50-20, bajo la acción de cargas estáticas y considerando diferentes niveles de inflado.
