INTRODUCCIÓN
La compactación es un proceso de degradación física muy común en los suelos dedicados a las actividades agrícolas (Reyes, 2010). Esta provoca el incremento de la densidad aparente del suelo según Reyes (2014) y destruye la estructura del mismo. De esta forma, influye en la disminución de la macroporosidad, lo cual suscita un desarrollo más débil del sistema radical, por lo que afecta el crecimiento vegetativo y los rendimientos de los cultivos (Gutiérrez et al., 2014).
La resistencia del suelo a la penetración ha sido utilizada con frecuencia en las investigaciones agronómicas para la detección de capas compactadas según Tussin et al. (2012), por el efecto de la mecanización agrícola Mazurana et al. (2013), los sistemas de manejo Marasca et al. (2015); Rodríguez et al. (2017, 2017) y el uso del suelo Dos Santos et al. (2015); Neiva et al. (2015), pues resulta conocida la relación directamente proporcional entre la resistencia a la penetración y la densidad del suelo Blanco (2009) y se considera un parámetro importante a la hora de evaluar la calidad física del suelo, las posibilidades de desarrollo de las raíces de las plantas y en el estudio de la dinámica del agua en el suelo (De Oliveira et al., 2010).
Así, la fuerza por unidad de área necesaria para la penetración del cono puede ser determinada a partir de equipos conocidos como penetrómetros (Soil Science Society of America, 2008). Los penetrómetros de impacto o dinámicos registran la resistencia a la penetración en número de impactos necesarios para atravesar una profundidad determinada Stolf (1991) por lo que es necesario realizar la conversión de dichos valores en resistencia mecánica del suelo para un mejor aprovechamiento de los datos obtenidos (De Oliveira et al., 2010; Giroldo y Rodrigues, 2014).
De esta manera, Betancourt et al. (2009) han elaborado ecuaciones a partir del modelo “Raíz de I”. Mientras que Dexter (1986) propone una fórmula que persigue el mismo objetivo. Vías un poco más sencillas han sido trabajadas por Stolf (1991) y suelo De Oliveira et al. (2010), al adaptar, a estos fines, las ecuaciones de los Holandeses, de Brix y de Sanders. Sin embargo, estos últimos han circunscripto sus trabajos al penetrómetro de impacto de Stolf et al. (1983), lo cual hace necesario el ajuste de estas ecuaciones a las características propias de otros penetrómetros de impacto en uso.
Los Vertisoles cultivados con caña de azúcar pueden ser afectados por la compactación inducida durante la cosecha mecanizada. Este factor edáfico limitante tiende a incrementarse de forma variable con el aumento de los ciclos del cultivo y es más notable en los entresurcos de las plantaciones (Sánchez et al., 2003).
El objetivo de este trabajo es evaluar tres modelos matemáticos utilizados en la transformación de los datos de campo obtenidos con un penetrómetro de impacto.
MÉTODOS
El trabajo se realizó en el año 2016 en un suelo clasificado como Vertisol Crómico según Hernández et al. (2015), plantado con caña de azúcar en el Bloque Experimental de Guaro, perteneciente a la Estación Provincial de Investigaciones de la Caña de Azúcar de Holguín. El muestreo se realizó con un penetrómetro de impacto, con el cual se determinaron la cantidad de impactos hasta 0,30 m de profundidad, en un transecto de 30,4 m de longitud y perpendicular a los surcos. Fueron muestreados 20 puntos cada 1,60 m, siempre en el centro del entresurco, por considerarse esta zona la de mayor afectación debido al tránsito de la maquinaria durante las actividades agrícolas.
Las determinaciones se realizaron con el suelo a capacidad de campo, de forma tal que, al prescindir del efecto de la humedad, la resistencia a la penetración se debe solo a las consecuencias de la compactación (Sellés et al., 2012). Para la transformación de los datos obtenidos (impactos por profundidad) se tuvieron en cuenta los siguientes modelos (Stolf, 1991; De Oliveira et al., 2010):
Modelo de los Holandeses:
Modelo de Sanders:
Modelo de Brix:
donde: F es fuerza de resistencia del suelo (kgf), M es masa impactadora (kg); m es masa del penetrómetro sin la masa impactadora (kg); g es la constante de aceleración de la gravedad (en m s-2); h es el recorrido de la masa impactadora (altura, en cm) y x es la penetración provocada por un impacto (cm impacto-1). El penetrómetro de impacto (Figura 1) tiene las siguientes características: M = 1 kg (Mg = 1 kgf); m = 3,5 kg (mg = 3,5 kgf); (M+m)g = 4,5 kgf; M/(M+m) = 0,222 kg; h = 45 cm.

FIGURA 1.
Penetrómetro de impacto utilizado en el estudio.
Al sustituir con estos valores, divididos por el área de la base del cono de la punta del penetrómetro (A=1,29 cm2) y considerar que en la práctica se sustituye x (penetración por impacto, en cm) por el inverso N (impactos por dm), de esta forma x = 10/N y que g = 9,81 m s-2; 1 kgf cm-2 = 9,81/100 MPa = 0,0981 MPa, se obtienen las ecuaciones siguientes:
Modelo de los Holandeses:
Modelo de Sanders:
Modelo de Brix:
Se realizó un análisis exploratorio de datos utilizándose, para la descripción univariada, los principales estadígrafos de posición y de dispersión. Se tuvieron en cuenta la cantidad de impactos en la capa de 0-30 cm de profundidad, los impactos por dm, la penetración por impacto y los valores de resistencia a la penetración obtenida a partir de los tres modelos. Se utilizó el coeficiente de correlación de Pearson entre los valores obtenidos por el modelo de los Holandeses y los de Sanders y de Brix; y entre la penetración por impacto y la resistencia a la penetración obtenida por los modelos. Para el procesamiento de los datos se empleó el software Statistica 7.
RESULTADOS Y DISCUSIÓN
La Tabla 1 muestra el análisis exploratorio de datos, realizado con los principales estadígrafos de posición y de dispersión a la información obtenida en el campo con el penetrómetro y los posteriores resultados de la transformación de los impactos por profundidad. Puede apreciarse que la media de los impactos necesarios para penetrar la capa de 0-30 cm de profundidad fue de 53,30, con un rango de 67 impactos, entre el valor mínimo y el máximo. Así también, la media de los impactos por dm y de la penetración por impactos fue de 17,64 y de 0,61 cm (esta unidad de medida solo para este último valor), respectivamente. El coeficiente de variación es de un 30,36% para la primera variable mencionada y de un 30,52%, en el caso de la segunda. Para la penetración por impacto el coeficiente de variación es un 25,43%.
En el caso de los estadígrafos de los modelos matemáticos se observa que con el modelo de Sanders se obtiene la mayor media de la resistencia a la penetración y que con este modelo se obtiene un mayor rango de valores. Por lo tanto, son mayores la desviación estándar, la varianza y el error estándar de los datos obtenidos. La menor media se obtuvo con el modelo de Brix, que muestra las menores desviación estándar, varianza y error estándar.
TABLA 1.
Estadígrafos de posición y de dispersión de los datos del penetrómetro de impacto y de la resistencia a la penetración obtenida a partir de los tres modelos
Desv. estándar: Desviación estándar; C. V.: Coeficiente de variación. Pen. por impacto: Penetración por impacto.
Este comportamiento de las medias (Sanders>Holandeses>Brix), coincide con lo obtenido por Stolf (1991), al considerar que con respecto al modelo de los holandeses, el modelo de Sanders sobreestima los valores de resistencia a la penetración, mientras que con el modelo de Brix dichos valores quedan subestimados. Este comportamiento de la resistencia a la penetración, según el modelo de Sanders, está dado por considerar el impacto de los componentes del penetrómetro como perfectamente elástico, sin pérdidas de energía; factor que si se tiene en cuenta en los otros dos modelos (M/M+m). En cuanto a los porcentajes del coeficiente de variación de la resistencia a la penetración obtenida a partir de los tres modelos, los mismos se encuentran dentro del rango permisible para trabajos agronómicos y ganaderos, pues según Espino y Arcia (2009) deben oscilar entre 10 y 30%.
Si bien desde el punto de vista experimental, el modelo de los Holandeses no cumple con todos los requisitos, desde una perspectiva teórica Stolf (1991) considera que en esta ecuación se tiene en cuenta la pérdida de energía durante el choque entre la masa del penetrómetro y la masa impactadora, al considerarse un choque totalmente inelástico, sin deformaciones permanentes.
Al considerar los valores obtenidos con el modelo de los Holandeses, la resistencia a la penetración en el camellón del área plantada con caña de azúcar se encuentra en las categorías de alto (2-4 MPa) y muy alto (4-8 MPa), de acuerdo con la clasificación de Arshad et al. (1996).
La Figura1 muestra la relación lineal y directa entre la resistencia a la penetración por el modelo de los Holandeses y la obtenida con los modelos de Sanders y Brix. Ambos modelos muestran, con respecto al de los holandeses, una correlación igual a 1, que se considera positiva perfecta.
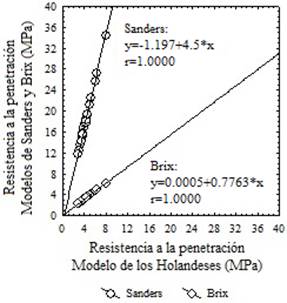
FIGURA 1.
Relación entre la resistencia a la penetración obtenida por los tres modelos.
De Oliveira et al. (2010) al considerar una situación hipotética en la que la penetración por impacto sea infinita, mientras utilizan un penetrómetro de impacto de 7,5 kgf cm-2 con la masa impactadora regulada a 40 cm de altura, encontraron teóricamente resistencias a la penetración mínimas extremas de 0,77 MPa con el modelo de los Holandeses. Mediante el mismo modelo, adaptado a las características del penetrómetro utilizado en este trabajo, es posible determinar valores de resistencia a la penetración por debajo del límite encontrado por los autores antes mencionados; aunque en la práctica dichos valores no sean factibles.
La Figura 2 muestra que existe una relación exponencial e inversa entre la resistencia a la penetración obtenida por los tres modelos y el avance por impacto. En el caso de los resultados obtenidos con el modelo de los Holandeses, cuando aparece la menor resistencia a la penetración (2,850 MPa), el penetrómetro de impacto utilizado avanza 0,91 cm; necesitándose 33 impactos para deformar el suelo hasta los 30 cm de profundidad, a razón de 11,00 impactos por dm.
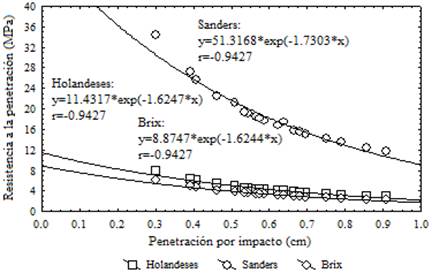
FIGURA 2.
Relación entre la penetración por impacto y la resistencia a la penetración en MPa.
En el punto de mayor compactación (7,942 MPa), el avance por impacto fue de 0,30 cm. Este valor fue obtenido a partir de los 100 impactos necesarios para penetrar la capa de 0-30 cm, lo que representó una cifra de 33,33 impactos por dm.
CONCLUSIONES
La aplicación del modelo de los Holandeses con las particularidades del penetrómetro de impacto utilizado genera la ecuación: RP (MPa)= 0,342+0,076 N
El modelo de Sanders sobreestima los valores de resistencia a la penetración (18,571 MPa), comparado con los resultados obtenidos con el modelo de los Holandeses (4,393 MPa). Mientras que con el modelo de Brix, la resistencia a la penetración (3,411 MPa) queda por debajo del segundo modelo mencionado.
Los valores de resistencia a la penetración obtenidos con el modelo de los Holandeses pueden clasificarse dentro de las categorías de altos y muy altos.
Existe una relación exponencial e inversa entre la penetración por impacto y la resistencia a la penetración obtenida a partir de los tres modelos.
