INTRODUCCIÓN
En el proceso de producción de granos y semillas la operación de trilla o descascarado, es decir, la separación de las semillas de las espigas, vainas o cápsulas, tiene gran importancia, ya que de ella depende el máximo aprovechamiento del producto cosechado. Para su realización en el mundo se han desarrollado múltiples y diversos dispositivos y máquinas de mayor o menor complejidad, pero por lo general son costosas. Para las pequeñas superficies de producción, la inversión en máquinas cosechadoras de las que oferta el mercado, por lo general no resultan rentables y la tendencia actual es la fabricación de pequeñas máquinas o descascaradores para productores con bajo poder adquisitivo (Duraisamy y Manian, 1990; Cabral-de França et al., 2013). El modelado matemático es una herramienta necesaria en el desarrollo de una máquina agrícola. El comportamiento de ésta se simula en diferentes condiciones de funcionamiento antes de que entre en la línea de producción, se reducen los costos, el tiempo necesario en el diseño, el número de prototipos que se construyen y las pruebas experimentales a realizar. Por lo tanto, equipos más eficientes técnicamente y a menor costo pueden ser desarrollados y optimizados.
Para el modelado y desarrollo de los órganos trilladores son fundamentales las propiedades físico-mecánicas del material a trillar, como son: contenido de humedad de la planta, relación grano-paja del material a cosechar, peso medio de los tallos, hojas y granos, dimensiones de las plantas y de los granos, coeficiente de fricción entre capas del material a trillar y de éste con el material con el que se fabrica el órgano trillador, fuerza de inserción grano-espiga, etc. Otros parámetros a tomar en cuenta son de tipo cinemático y dinámico, que determinan el efecto de los órganos de trabajo sobre el material a trillar y la energía que se consume en el proceso. Los más significativos son: velocidad periférica, diámetro, número de barras o hileras de dientes del cilindro, número y disposición de los dientes en las platinetas, longitud de trabajo del cilindro trillador, el momento de inercia del cilindro, la potencia necesaria para accionar el cilindro, así como el tipo y dimensiones del cóncavo.
Un modelo matemático es una descripción aproximada, expresada mediante simbología matemática, de alguna clase de fenómenos del mundo exterior (Singh, 2008). La simulación matemática es un método de conocimiento, pronóstico y control (Tarasiévich, 2004). La construcción del modelo matemático consta de 4 etapas: 1) Formulación de las leyes que relacionan a los objetos principales del modelo; 2) Investigación del problema matemático; 3) Comprobación de la coherencia del modelo con la realidad; y 4) Análisis del modelo y su modificación.
La calidad de trabajo de los órganos trilladores se evalúa por el número de granos sin trillar y por los daños mecánicos que éstos sufren en el proceso de trilla. Finalmente, y de gran relevancia resulta el tener en consideración aspectos relacionados con la capacidad de procesamiento del órgano trillador y con la energía que consume el proceso, que debe estar en correspondencia con el punto crítico de menor costo de la trilla para la productividad deseada. El grano dañado durante la trilla está relacionado a la energía absorbida por el grano durante el impacto del órgano de trabajo en el cultivo (Huynh et al., 1982a, 1982b).
El presente trabajo tiene como objetivo desarrollar y evaluar un modelo, para predecir la eficiencia del descascarado, cápsulas no descascaradas y el daño mecánico del grano de una máquina descascaradora de higuerilla.
MÉTODOS
Los modelos matemáticos se desarrollaron en el Laboratorio de Cómputo del Postgrado de Ingeniería Agrícola y Uso Integral del Agua de la Universidad Autónoma Chapingo y la evaluación se realizó en las instalaciones del Centro Nacional de Estandarización de Maquinaria Agrícola del Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. La metodología a utilizar en el trabajo es la propuesta por: Huynh et al. (1982a, 1982b); Souza et al. (1998); Queiroz et al. (2004); Ndirika (2005, 2006); Simonyan et al. (2010); Ndukwu y Asoegwu (2011).
Desarrollo teórico de los modelos
El descascarado implica toda acción desde la entrada del material por la tolva, la cámara de descascarado hasta la salida. Los parámetros físicos que afectan al proceso de descascarado incluyen las propiedades físicas del cultivo y los parámetros de la máquina son: 1) Las propiedades del cultivo: variedad, edad, contenido de humedad de la cápsula, densidad aparente y diámetro geométrico medio del fruto; 2) Las propiedades de la máquina: velocidad de avance, diámetro de la cámara de descascarado, velocidad del disco, y capacidad de procesamiento.
En el desarrollo del modelo se hicieron los siguientes supuestos: 1) El contenido de humedad de la cáscara y la semilla es la misma; 2) La dimensión de la cápsula es constante y con el mismo contenido de humedad; 3) El grosor de la cáscara es constante y con el mismo contenido de humedad, 4) El diámetro del cóncavo para el descascarado es variable; 5) La distancia u holgura entre el disco de descascarado y el cóncavo se fija en la parte media; 6) La edad de las cápsulas es la misma; 7) El peso individual y el volumen de la cápsula es constante a un contenido de humedad particular; 8) La velocidad del órgano de descascarado es la misma que la del eje motriz; 9) La velocidad del eje es fija; 10) La carga de compresión de los frutos es uniforme en toda la superficie del órgano de descascarado.
Con base en los supuestos anteriores las principales variables de importancia del modelo son: el contenido de humedad de la cápsula, la densidad aparente del fruto, la densidad de las partículas de la cápsula, la tasa de alimentación, la capacidad de procesamiento y la velocidad de descascarado.
Modelo de la eficiencia del descascarado
La principal función del órgano de descascarado es separar la cáscara del grano, esta se calcula:
donde:
H
- descascarado del grano, %;
a y b
- coeficientes de la ecuación para la alimentación de granos aleatoriamente, adim.;
x
- holgura entre el disco y el cóncavo, mm.
Para un adecuado descascarado del fruto en el mecanismo, se debe cumplir la condición:
En la Figura 1 se muestra el proceso de descascarado del fruto entre la periferia del disco y la holgura del cóncavo variable.
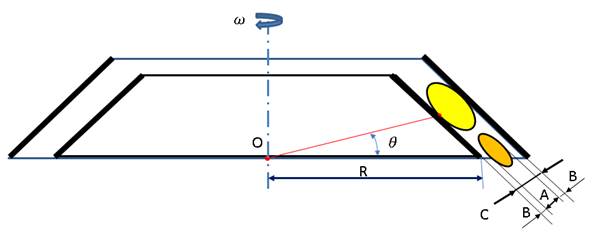
FIGURA 1.
Descascarado del carpelo de higuerilla entre el disco y el cóncavo. R- radio mayor del disco, C- holgura entre disco y cóncavo, A- anchura del grano de higuerilla, y B- espesor de la cascara del carpelo de higuerilla.
Modelo del grano dañado
La acción de la máquina sobre el producto durante la cosecha puede ser responsable por provocar daños mecánicos a los granos, constituyendo la trilla la más importante fuente de daños. Durante la cosecha, la ocurrencia de daños mecánicos depende principalmente de la humedad de los granos y de la velocidad periférica del cilindro trillador (Souza et al., 1998).
La presencia de daños mecánicos en los granos cosechados mecánicamente es inevitable. Esto puede perjudicar la calidad de los granos, disminuyendo considerablemente su valor de mercado. A pesar de las necesidades específicas de cada productor, los daños mecánicos pueden ser altamente perjudiciales al producto final. Cuando los daños mecánicos son visibles, con granos partidos y con rupturas en la cáscara, pueden ser separados por los sistemas de limpieza.
El modelo de grano dañado propuesto es:
Calibración y validación del modelo
Los modelos de la eficiencia del descascarado y grano dañado se verificaron con el fin de confirmar su coherencia con los resultados experimentales de una descascaradora. El estudio se llevó a cabo en una maqueta experimental descascaradora de higuerilla (Figura 2) y los valores, obtenidos con el modelo, se compararon con los datos experimentales.

FIGURA 2.
Maqueta experimental de descascarado.
Determinación de los parámetros de validación
Para la validación del modelo se tomarán en cuenta los siguientes parámetros:
Contenido de humedad: La validación del modelo se realizó con un solo contenido de humedad. El contenido de humedad del grano se determinó en una estufa a una temperatura de 75°C durante 24 h. El contenido de humedad se calculó en base húmeda.
Eficiencia de descascarado: Es la relación de la masa de las cápsulas completamente descascarada y de las no descascaradas entre la masa total de las cápsulas introducidas en la tolva. Se calcula como:
donde:
ED- eficiencia del descascarado, %;
WT- masa total de las cápsulas de higuerilla que se introducen en la tolva, kg;
X- masa de las cápsulas de higuerilla parcialmente descascaradas y no descascaradas, kg.
Relación de granos dañados: Este es un factor que cuantifica la cantidad de granos dañados y descascarados, de las cápsulas descascaradas recibidas. Se calcula así:
Instrumentación y equipo de medición
Los datos generados a partir de la máquina descascaradora estacionaria de higuerilla utilizada en la verificación del modelo de la capacidad de producción fueron medidos o evaluados por los siguientes métodos:
Medición de la masa: Una balanza de precisión marca Ohaus con 0,01g de precisión se utilizó en el pesaje del material de estudio.
Determinación del contenido de humedad: El contenido de humedad del cultivo se determinó por el método de la estufa marca Lab-Line Instruments a una temperatura de 75º C durante 24 horas.
Medición de la velocidad: Un contador de revoluciones (tacómetro) marca Lutron modelo DT-2230 se utilizó para calibrar la velocidad del órgano descascarador. Mediante un variador de frecuencia marca Danfoss modelo VLT se reguló la velocidad del motor trifásico de 3 hp marca ABB.
Medición de la longitud: Un calibrador de lainas marca Truper y un vernier marca Mitutoyo se utilizaron para medir la holgura entre el cilindro y el cóncavo. La calibración de la holgura se realizó de 8 a 14 mm con variaciones de un mm en la descascaradora.
Medición de la eficiencia del descascarado, grano dañado y no descascarado: En la tolva de alimentación de la máquina se introducen 3 kg de cápsulas de higuerilla, se colecta todo el material en la salida de ésta. Manualmente se separan el material descascarado, no descascarado y dañado.
RESULTADOS Y DISCUSIÓN
Calibración del modelo de la eficiencia del descascarado y grano no descascarado
De una maqueta experimental se obtuvieron los datos experimentales y mediante una regresión lineal se obtuvieron los coeficientes a=-7,7156 y b= 161,57 con R2=0,93 y 5,02 de error estándar (Figura 3). Para el grano no descascarado se obtuvo a=7,5156 y b=- 61,567 con R2= 0,93 y 5,02 de error estándar (Figura 4). A medida que se disminuye la separación entre el disco y el cóncavo aumenta la eficiencia de trilla, la cual debe estar en función de las dimensiones de los carpelos de las cápsulas de higuerilla. Caso contrario ocurre al aumentar la holgura disminuye la eficiencia del descascarado y aumenta la cantidad de carpelos sin descascarar por el órgano de trabajo.
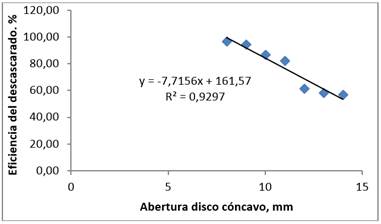
FIGURA 3.
Eficiencia del proceso de descascarado a 120 rpm.
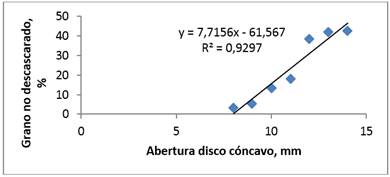
FIGURA 4.
Grano no descascarado en el órgano de descascarado a 120 rpm.
Calibración del modelo de grano dañado
De una maqueta experimental se obtuvieron los datos experimentales y mediante una regresión se obtuvieron los coeficientes de la ecuación de potencia A=35425 y n=-4,192 con R2=0,95 y 0,95 de error estándar (Figura 5). El grano dañado aumenta al disminuir la holgura entre el disco y el cóncavo, pero también está en función de la velocidad del órgano de trabajo. A mayor velocidad del mecanismo de descascarado se tienen mayores daños mecánicos del producto. Es importante también considerar, el contenido de humedad del material, ya que a medida que este disminuye, aumenta el daño mecánico.
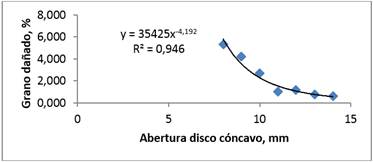
FIGURA 5.
Grano dañado del proceso de descascarado.
Validación del modelo
Los modelos matemáticos fueron validados usando datos generados de un prototipo de máquina descascaradora. Los modelos se hicieron para una frecuencia de rotación de 120 min-1, con separaciones entre el disco y el cóncavo desde 8 a 14 mm con variación de 1 mm. En el Cuadro 1 se muestran los parámetros geométricos principales de la descascaradora de higuerilla.
CUADRO 1.
Datos del cilindro y cóncavo de la descascaradora
Validación del modelo de la eficiencia del descascarado y grano no descascarado
El modelo de predicción de la eficiencia del descascarado y grano no descascarado se simuló en el software de Matlab y de las pruebas experimentales a 120 rpm de la máquina descascaradora. De la Figura 6 se observa, que el valor estimado por el modelo y el experimental tienen una correlación alta con R2 de 92,97 % con un error estándar de 4,74. Al comparar las variaciones de la eficiencia del descascarado medido y simulado (Cuadro 2) se obtuvo un rango de desviación absoluta de 3,90%, con un error estándar y relativo de 4,26% y -0,34% respectivamente. La desviación de la media tiene un rango de 0,0779%, lo que indica que el modelo tiende a una ligera variación en la eficiencia del descascarado.
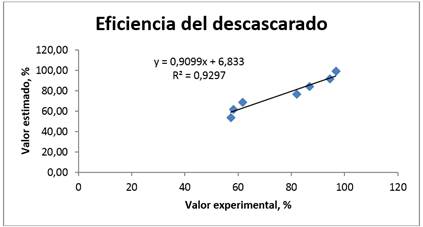
FIGURA 6.
Eficiencia del descascarado medido y experimental a 120 min-1.
De la Figura 7 se observa, que el valor estimado y el experimental para las cápsulas no descascaradas tienen una correlación alta con R2 de 92,97 % con un error estándar de 4,74. De la comparación de la variación del grano no descascarado observado y simulado (Cuadro 3) se obtuvo la desviación absoluta de 3,90%, con un error estándar y relativo de 4,26% y -0,41% respectivamente. La desviación de la media tiene un rango de -0,0785%, lo que muestra que el modelo tiene una ligera variación en cuanto al grano no descascarado por el órgano de trabajo.
Los resultados demuestran que a pesar que en los dos modelos no se tiene en cuenta la velocidad de trabajo del órgano de descascarado y el contenido de humedad, las estimaciones logradas son lo suficientemente adecuadas como para poder emplear el modelo en el diseño de máquinas agrícolas.
CUADRO 2.
Eficiencia del descascarado estimada y experimental para 120 min-1
| Abertura disco cóncavo, mm | Eficiencia del descascarado, % | |
|---|---|---|
| Experimental | Estimada | |
| 8 | 96,65 | 99,27 |
| 9 | 94,57 | 91,72 |
| 10 | 86,59 | 84,17 |
| 11 | 82,01 | 76,62 |
| 12 | 61,64 | 69,07 |
| 13 | 58,18 | 61,52 |
| 14 | 57,22 | 53,96 |
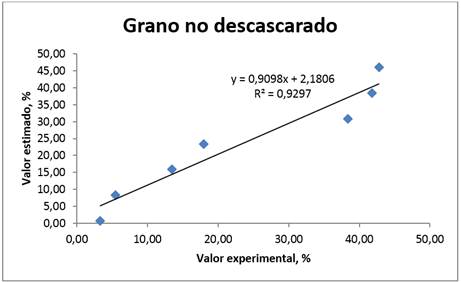
FIGURA 7.
Grano no descascarado estimado y experimental a 120 min-1.
CUADRO 3.
Grano no descascarados estimado y experimental para 120 rpm
Validación del modelo de grano dañado
El modelo de predicción del grano dañado se simuló en el software de Matlab y las pruebas experimentales se realizaron a 120 rpm en la máquina descascaradora. De la Figura 8 se observa, que el valor estimado y el experimental tienen una correlación alta con R2 de 94,92 % con un error estándar de 0,39. De la comparación de la variación del grano dañado mecánicamente observado y simulado (Cuadro 4) se obtuvo la desviación absoluta de 0,27%, con un error estándar y relativo de 0,36% y -3,98% respectivamente. La desviación de la media tiene un rango de 0,0697%, lo que muestra que el modelo tiene una ligera variación en cuanto al grano dañado por el órgano de trabajo.
Además se determinó el contenido de humedad de la cápsula, teniendo un máximo del 5,58%, mínimo de 5,26%, media del 5,43% y desviación estándar de 0,12%.
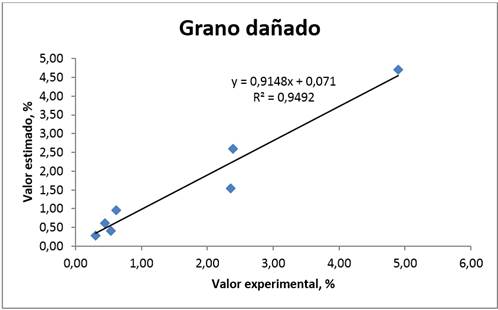
FIGURA 8.
Grano dañado medido y experimental a 120 min-1.
CUADRO 4.
Grano dañado estimado y experimental para 120 min-1
| Abertura disco cóncavo, mm | Grano dañado, % | |
|---|---|---|
| Experimental | Estimado | |
| 8 | 4,90 | 4,70 |
| 9 | 2,39 | 2,60 |
| 10 | 2,36 | 1,53 |
| 11 | 0,62 | 0,95 |
| 12 | 0,45 | 0,61 |
| 13 | 0,54 | 0,41 |
| 14 | 0,31 | 0,28 |
Los resultados experimentales de los tres modelos están de acuerdo a lo planteado por Srivastava et al. (2006) para el órgano de trabajo de las cosechadoras de granos.
Cuando las medias de la eficiencia del descascarado y cápsula no descascarada estimada y medida se compararon estadísticamente, reveló que no hubo diferencia significativa entre estas al nivel de significancia del 5%, como se muestra en el Cuadro 5. De manera análoga para las medias del grano dañado al ser comparadas con una prueba “t”, demostró que no hubo diferencia significativa entre ellas al nivel de significancia del 5%, como se muestra en el Cuadro 5.
CUADRO 5.
Parámetros de validación de los modelos de la eficiencia del descascarado, grano no descascarado y dañado con los datos experimentales de la descascaradora de higuerilla en el nivel de significación p ≤ 0,05
CONCLUSIONES
Tres modelos matemáticos se desarrollaron para describir la eficiencia del descascarado, grano no descascarado y grano dañado de una maqueta experimental para descascarar las cápsulas de higuerilla. El modelo fue validado con los datos experimentales obtenidos de la maqueta experimental. Las variables del modelo fueron la velocidad del órgano de descascarado y la holgura del disco y el cóncavo. Un coeficiente de correlación alto (R2=0,9297) a un nivel de significancia del 5% indicó que la combinación de las ecuaciones mediante la suma de los componentes es apropiada para los modelos de eficiencia del descascarado y cápsula no descascarada, mientras que para el caso del grano dañado fue R2= 0,9492.
