Una de las contribuciones más importantes a la metodología estadística en la década de los años 50, fue dada por (Box y Hunter, 1957; Box y Draper, 1959; Box y Wilson, 1992), al desarrollar criterios teórico-metodológicos para aportar una mayor precisión en la respuesta de diferentes procesos sometidos a la influencia de uno o varios factores analizados, aspecto que es generalmente conocido como ¨Metodología para el estudio de Superficies de Respuesta¨ (MSR, en inglés RSM).¨
Los autores antes mencionados señalan que además del modelo, es necesaria una adecuada elección de los tratamientos, lo que implica una búsqueda de la combinación Modelo-Diseño de tratamientos, que es en esencia lo que recoge la MSR.
Según Cuesta (2012), durante los últimos 20 años esta metodología ha tenido un desarrollo considerable tanto en aspectos teóricos como en aplicaciones en escenarios reales. Inicialmente debutó con éxito en la industria química y últimamente ha encontrado amplia aplicación en procesos de fabricación de semiconductores, aparatos electrónicos, maquinado, corte de metal y procesos de ensamble, lo cual se refleja en varias publicaciones.
En la literatura consultada en Cuba se evidencian pocas investigaciones con aplicaciones de la MSR; en particular en el ámbito agropecuario Guerra (1980), la empleó para la determinar dosis óptimas de fertilización N, P, K con experimentos de campo. Posteriormente en la rama agrícola (Miranda et al, 2013), la utilizaron en estudios relacionados con la protección de plantas. En tal sentido resulta necesario divulgar un conjunto de aspectos vinculados con esta metodología por el potencial de aplicaciones que puede tener en el ámbito agropecuario y ciencias afines.
Considerando lo expuesto anteriormente, el objetivo de este trabajo es reseñar los criterios teórico-prácticos y metodológicos sobre la Modelación Matemático-Estadística relacionada con la Metodología de Superficie de Respuesta y sus aplicaciones agrarias y en otras ramas.
La MSR es un conjunto de técnicas utilizadas en el estudio de la relación entre una o más respuestas y un conjunto de factores o variables independientes, donde el objetivo es optimizar ésta(s) respuesta(s). Esta metodología se realiza mediante una experimentación secuencial, esto es, la aproximación a la región de interés se realiza de forma iterativa utilizando diseños cada vez más complejos, que dependen de la información que se obtiene en cada etapa (Figueroa, 2003).
Teniendo en consideración los criterios aportados por (López, 1988 y Kuehl, 2001), la MSR es de utilidad para resolver ciertos tipos de problemas científicos, procesos industriales y de ingeniería, mostrándose con mayor aplicación en el área industrial, química y agrícola.
La superficie de respuesta permite que el investigador inspeccione, de manera visual, la respuesta para cierta zona de los niveles de los factores de interés y evaluar su sensibilidad a los factores de tratamiento. En ciertas aplicaciones industriales, las superficies de respuesta se exploran para determinar la combinación de niveles de los factores que proporcionan una condición operativa óptima, como la combinación de temperatura y tiempo que maximiza la producción química. En otras aplicaciones, se exploran para encontrar la combinación de niveles de los factores que proporcionan mejoras económicas a las respuestas de las condiciones operativas urgentes, si no es demasiado costoso lograr esas condiciones óptimas (Kuehl, 2001).
El autor antes mencionado se refiere a que las superficies de respuesta se pueden utilizar en estudios analíticos de procesos fundamentales y pone como ejemplo las ciencias biológicas para investigar la influencia mutua de los factores sobre la variable respuesta, como la interacción entre el nitrógeno y el fósforo en el crecimiento de las plantas.
Diferentes autores, entre ellos (Kuehl, 2001 y Figueroa, 2003), señalan que la representación matemática de los modelos de MSR puede ser de diversas formas. Si todos los factores de una investigación, como tiempo, temperatura, niveles de fertilización, etc., se puede pensar que la variable respuesta Y es una función de los niveles de estas variables, que se puede expresar como:η
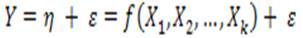
Y:
está influido por los niveles de k factores representados por las variables cuantitativas: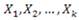 
, lo que significa que existe una función
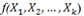que proporciona el correspondiente valor de η para alguna combinación dada de niveles:
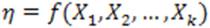
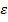mide el error experimental asociado con las diferentes combinaciones de los niveles de las variables consideradas. El error experimental en general se asume que sigue una distribución normal con media 0 y desviación estándar σ, que puede indicarse por ε ~ N (0, σ2)
A la función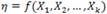 
se le conoce como superficie de respuesta.
A todo el procedimiento de aproximación a la función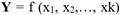 
+ ε, se le llama MRS.
Cuando no se conoce la forma matemática de η la función puede aproximarse de forma satisfactoria dentro de la región experimental, por un polinomio de las variables X. En particular (Cuesta, 2012), se ha referido a polinomios de primer y segundo grados, que se pueden representar como sigue:
Los autores de este trabajo coinciden con (Box y Hunter, 1957), en la clasificación de los modelos de superficie de respuesta, considerando dos variables o factores y pueden ser generalizados a más de dos.
Modelo lineal de primer orden sin interacción (o producto cruzado)
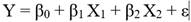
Modelo lineal de primer orden con interacciones
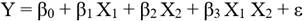
Modelo cuadrático o de segundo orden
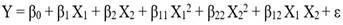
En general el modelo de superficie se puede escribir como:
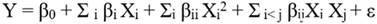
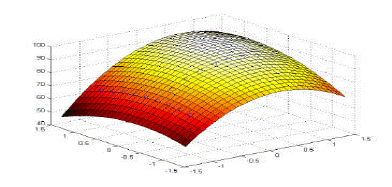
La superficie de respuesta y sus curvas de nivel o contornos(líneas con valores iguales de respuesta), podrían representar diferentes gráficas, según la superficie de respuesta obtenida sea lineal o cuadrática. En la Figura 1 se presentan un caso de superficie cuadrática, tomada de (Ferré y Rius, 2017), la cual representa la presencia de un punto de máximo.
Los gráficos de las superficies pueden sugerir la presencia de puntos de mínimo o máximo, pendiente ascendente o cresta elevada o punto de silla
En la implementación y análisis de los resultados originados por la aplicación de la MSR, es necesario considerar un conjunto de aspectos de la Matemática y la Estadística, que se pueden resumir en:
Aspectos matemáticos: Análisis de funciones Algebra matricial, Cálculo Diferencial para analizar los diferentes métodos en la determinación las condiciones óptimas, la Geometría analítica en el análisis de la forma y contornos de la superficie y la Investigación Operacional con criterios alternativos en la determinación de las condiciones óptimas del proceso investigado.
Aspectos estadísticos: diseños de tratamientos (Factoriales completos y fraccionados, Diseños para superficies de respuesta y criterios para la validación del modelo, entre otros aspectos.
Por otra parte para realizar él análisis sobre la validez estadística de la superficie de respuesta obtenida, se pueden seguir los criterios dados por (Guerra et al., 2003).
(Ferré y Rius, 2017), se refieren al Diseño Estadístico de Experimentos o también denominado Diseño Experimental, como una metodología basada en herramientas matemáticas y estadísticas, cuyo objetivo es ayudar al investigador a:
Seleccionar la estrategia experimental óptima que permita obtener la información buscada con el mínimo costo.
Evaluar los resultados experimentales obtenidos, garantizando la máxima fiabilidad en las conclusiones que se obtengan.
La literatura especializada, denomina en general a los diseños asociados a las superficies de respuesta, como diseños de primer y segundo orden respectivamente.
De acuerdo con criterios aportados por los autores que originaron esta metodología y de otras publicaciones en que se combina la teoría con las aplicaciones a problemas concretos de la práctica investigativa, se resumen en fases o pasos los principales aspectos a considerar para conforman la MSR:
Fase 1. Al comienzo del estudio de una superficie de respuesta, se explora la región de respuesta óptima, mediante experimentos factoriales completos 2 k o factoriales fraccionarios 2 k − p , con el fin de estimar las respuestas medias para un modelo de primer orden. En general se recomienda agregar dos o más repeticiones a la combinación de los niveles medios de cada uno de los factores para estimar el error experimental y poder valorar el buen ajuste del modelo.
Fase 2. Una vez que se identifica la región de respuesta óptima, debe diseñarse un nuevo experimento para caracterizar la superficie de respuesta. En general, la superficie se aproxima por medio de una ecuación cuadrática para determinar la curvatura de la superficie.
Los factoriales 2k o sus fracciones son diseños útiles para identificar los factores significativos y las regiones de respuesta óptima, pero no proporciona información suficiente para estimar las ecuaciones de respuesta cuadrática.
Fase 3. Una opción a lo anterior es utilizar factoriales 3k, que presenta el inconveniente de la cantidad de puntos experimentales requiere. Si k = 2 factores se necesitarían 9 combinaciones de tratamientos y si k = 3 factores, el experimento factorial 33 requiere 27 combinaciones de tratamientos y así sucesivamente un 34 requiere 81 tratamiento. Esta cantidad de tratamientos hace complejo el trabajo experimental, desde cualquier punto de vista, aunque está también la opción de usar un factoriales fraccionado 3 k - p.
Fase 4. Las opciones de uso de los factoriales 33, fueron dadas por (Box y Wilson, 1992), mediante los Diseños Compuestos Centrales (DCC). Existen varias clases de diseños desarrollados para la aproximación a una superficie de segundo orden, que no requieren tantas combinaciones de tratamientos como los factoriales 3k. En este diseño, los factores generalmente se codifican, para proporcionar un marco de trabajo uniforme al investigar los efectos de los factores. Los niveles codificados de un factor A de un diseño factorial 2 k son:
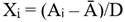
En general los niveles codificados del factorial quedan: nivel bajo de A: -1; nivel medio de A: 0 y nivel alto de A: 1
En la Tabla 1 se recoge la matriz con los códigos de los niveles de los factores para el DCC, considerando tres factores En general las coordenadas de los puntos axiales de los ejes de los factores codificados son: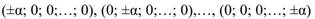 
y los puntos centrales son de la forma (0, 0, 0,...,0). El valor de α puede escogerse para hacer los coeficientes de regresión ortogonales o para minimizar el sesgo que puede producir la forma de la superficie de respuesta, estos se pueden obtener de la tabla 3. Cichran y CoxPara un DCN se puede confeccionar una tabla similar según sea la ubicación del punto en uno de los extremos del cubo.
La Tabla 2 propuesta por (Davies, 1954) y ampliada por (Guerra, 1980), recoge los componentes del DCC y el Factoriales completes 3k correspondientes, según el número de factores.
| No. | X2 | X2 | X3 | Y |
|---|---|---|---|---|
| 1 | -1 | -1 | -1 | Y1 |
| 2 | 1 | -1 | -1 | Y2 |
| 3 | -1 | 1 | -1 | Y3 |
| 4 | 1 | 1 | -1 | Y4 |
| 5 | -1 | -1 | 1 | Y5 |
| 6 | 1 | -1 | 1 | Y6 |
| 7 | -1 | 1 | 1 | Y7 |
| 8 | 1 | 1 | 1 | Y8 |
| 9 | -1,215 | 0 | 0 | Y9 |
| 10 | 1,215 | 0. | 0 | Y10 |
| 11 | 0 | -1,215 | 0 | Y11 |
| 12 | 0 | 1,215 | 0 | Y12 |
| 13 | 0 | 0 | -1,215 | Y13 |
| 14 | 0 | 0 | 1,215 | Y14 |
| 15 | 0 | 0 | 0 | Y15 |
En esta tabla se puede apreciar la amplia diferencia entre la cantidad de puntos experimentales del DCC y el factorial complete 3k, aspecto que indica que la MSR además de propiciar la determinación de las condiciones óptimas en que operan determinados procesos, permite hacerlo con menos puntos experimentales que los tradicionales factoriales completos.
(Figueroa, 2003), señala que el Diseño Compuesto Central Rotacional (DCR), se considera que es un DCC en que la condición de notabilidad se establece considerando que la varianza de los valores estimados sea constante en puntos equidistantes del centro del diseño. Esta condición se aplica a factoriales completos y fraccionados.
La Tabla 3 recoge la matriz con los códigos de los niveles de los factores para el DCR y la Tabla 4 propuesta por (Box y Hunter, 1957) y ampliada por (Guerra, 1980), recoge los componentes del DCR y de Factoriales completes 3k correspondientes, según el número de factores.
(Kuehl, 2001) plantea que las propiedades de los diseños experimentales convenientes para la estimación de superficies de respuesta, incluyen la capacidad para estimar el error experimental y tener en cuenta una prueba de la falta de ajuste del modelo. Los diseños también deben proporcionar estimaciones eficientes de los coeficientes del modelo y predecir las respuestas.
| No. | X2 | X2 | X3 | Y |
|---|---|---|---|---|
| 1 | -1 | -1 | -1 | Y1 |
| 2 | 1 | -1 | -1 | Y2 |
| 3 | -1 | 1 | -1 | Y3 |
| 4 | 1 | 1 | -1 | Y4 |
| 5 | -1 | -1 | 1 | Y5 |
| 6 | 1 | -1 | 1 | Y6 |
| 7 | -1 | 1 | 1 | Y7 |
| 8 | 1 | 1 | 1 | Y8 |
| 9 | -1,682 | 0 | 0 | Y9 |
| 10 | 1, 682 | 0. | 0 | Y10 |
| 11 | 0 | -1, 682 | 0 | Y11 |
| 12 | 0 | 1, 682 | 0 | Y12 |
| 13 | 0 | 0 | -1, 682 | Y13 |
| 14 | 0 | 0 | 1, 682 | Y14 |
| 15 | 0 | 0 | 0 | Y15 |
| 16 | 0 | 0 | 0 | Y16 |
| 17 | 0 | 0 | 0 | Y17 |
| 18 | 0 | 0 | 0 | Y18 |
| 19 | 0 | 0 | 0 | Y19 |
| 20 | 0 | 0 | 0 | Y20 |
(Kuehl, 2001)se refiere a las propiedades de los diseños experimentales más convenientes para la estimación de superficies de respuesta, incluyen la capacidad para estimar el error experimental y tener en cuenta una prueba de la falta de ajuste del modelo. Los diseños también deben proporcionar estimaciones eficientes de los coeficientes del modelo y predecir las respuestas.
El autor anterior señala que Box y Behnken en 1960 propusieron una clase de diseños de tres niveles para estimar las superficies de respuesta de segundo orden, estos diseños son rotatorios, o casi rotatorios, con menor número de unidades experimentales en comparación con los diseños 3k. Por otra parte (Cuesta, 2012), señala que en el DCR se supone que el experimento es completamente al azar, esto es, si las diferentes combinaciones de tratamiento se aplican una después de otra, el orden en la secuencia deberá ser al azar.
(Cuesta, 2012), indica sobre la MSR con respuestas múltiples, para lo cual se requiere en primer lugar construir un modelo de superficie de respuesta apropiado para cada respuesta y después intentar encontrar un conjunto de condiciones de operación que optimice ó brinde la mejor respuesta posible del conjunto de variables o características.
Este autor argumenta que un enfoque relativamente directo para optimizar varias respuestas, es cuando se tienen pocas (hasta 3) variables de respuesta y pocos factores (hasta 2), mediante la superposición de las gráficas de contorno independientes de cada respuesta en que el investigador efectúa una inspección visual para determinar alguna zona de intersección que brinde el mejor valor posible para las múltiples respuestas; ó al menos optimizar aquella variable que el investigador considera más importante, manteniendo las otras respuestas dentro de un rango de tolerancia.
En las condiciones de Cuba se reportan pocas publicaciones científicas relacionadas con la MSR y en particular en las ciencias agropecuarias. En esta área se reporta la investigación de (Guerra, 1980), con la colaboración del ICA e INCA, en busca de la relación modelo - diseño de tratamientos para la determinación de las dosis óptimas de fertilización N, P, K en los cultivos de la caña de azúcar, cítrico y pasto. En este caso en la región experimental correspondiente a factoriales completos 3k (k = 2, 3) en diseños de bloque al azar, se exploraron DCC y DCR (completos, con factoriales fraccionados 2k-1 y bloques incompletos). Se siguió un proceso de simulación por el Método de Monte Carlo.
Un resultado a señalar en esta investigación, es el buen ajuste mostrado por la superficie de respuesta de segundo orden en el DCC con factorial fraccionado 2k - 1(k = 3), en que solo se analizaron 11 tratamientos, frente a los 27 tratamientos del factorial completo 33.
En el Centro Nacional de Sanidad Agropecuaria (CENSA), se reporta el trabajo presentado por (Miranda et al., 2013), relacionado con la aplicación de la MSR para evaluar estabilidad en almacén de un agente de control biológico, publicado en la Revista Protección Vegetal. Los autores mediante un Análisis de Componentes Principales identificaron los factores de mayor incidencia y finalmente por medio de la MSR se obtuvo la combinación de porcentaje de relleno de zeolita y temperatura de almacenamiento que favoreció la germinación, utilizando un DCC con dos factores.
En el área de las Ciencias Químicas, Físicas y Farmacéuticas, se puede hacer referencia a la publicación de (López, 1988), en que se recogen aspectos teóricos y aplicaciones de la MSR.
En relación con otros países de América Latina, se encuentra la aplicación de la MSR dadas por: (Chacín, 1998; Gonzalez et al., 2006; Del Ángel et al., 2015), en investigaciones agrícolas.
En aspectos relacionados con la panificación, están los trabajos de (Milde et al., 2009), que mediante el análisis de la MSR determinaron la combinación óptima de grasa, huevo y leche en los rangos ensayados, que permitió obtener un panificado con propiedades de textura aceptables, utilizando el nivel intermedio de huevo y leche y el superior de grasa, al priorizar la disminución de la elasticidad por sobre la firmeza. Así como la aplicación de un DCR de dos factores dado por (Torres et al.,2016), para la evaluación de sedimentos de pulque (xaxtle), como cultivo iniciador para obtener un producto de panificación de bajo índice glucémico y obtener la cantidad óptima de xaxtle para la producción de pan.
Desde la década de los años 70, los autores han detectado la presencia de numerosas publicaciones sobre la MSR, en la Revista Agrociencia de México en lo teórico y con aplicaciones, y más reciente en lo fundamental en el área de la tecnología e ingeniería en las publicaciones de la Revista Technometrics en Journal of Quality Technology y el Journal of Statistical Software, así como textos especializados, que con frecuencia están escritos por los autores que desarrollaron esta metodología en la década de los años 50.
En los software estadísticos sobre Windows más tradicionales es posible procesar aplicaciones de la MSR, con el apoyo de una o más opciones de trabajo, que pueden ser complementadas con software matemáticos como el MATLAB, sobre todo en los gráficos para determinar los contornos de la superficie y el posible punto extremo, entre otros aspectos. Por otra parte resulta de gran interés en la actualidad las posibilidades que brinda el software libre.
(Figueroa, 2003), señala que en la actualidad hay varios paquetes estadísticos para analizar superficies de respuesta, algunos de estos específicamente diseñados para ello, que permiten un análisis muy completo de esta metodología.
La sección de Diseños de Experimentos en Statgraphics construye y analiza muchos tipos de experimentos. Estos incluyen diseños para investigación, diseños de optimización, experimentos con mezclas, diseño robusto del tipo dado por Taguchi, diseños D-Óptimos, y diseños para estudiar factores categóricos. El programa asiste al usuario en la construcción de los experimentos antes de que cualquier dato sea recolectado, analizando los datos una vez que los experimentos fueron desarrollados, aumentando el diseño si es necesaria más información, y en la determinación de condiciones óptimas una vez que el modelo estadístico fue desarrollado (Statgraphics Plus, 2006).
Se considera que (Lenth, 2009a, 2009b, 2010), aporta muy buenos criterios en sus artículos con orientaciones relacionadas con el uso de software especialmente para la MSR. Esta autora hace referencia a versiones del paquete rsm en forma gráfica y metodológica, y a la MSR usando el software (Schwinghamer y Pierre, 2017), hacen referencia al paquete ‘rsurface’: en un DCR.
(Torres et al., 2016), aplican la MSR con un DCR con el programa Design Expert 7.0 (Stat - Ease Inc. Minneapolis, MN, EE. UU.), se utiliza la herramienta de optimización D - óptima del Design Expert.
Los autores coinciden con (Cuesta, 2012), en que adicionalmente, para completar la validez estadística de superficies de respuesta de primer y segundo orden, se deben efectuar las respectivas pruebas a los residuos del modelo, tales como: Prueba de normalidad (Kolmogorov-Smirnov, Shapiro-Wilks, Anderson-Darling, etc.), Prueba de Independencia (Durbin-Watson) y Prueba de Homoscedasticidad.
Sobre la Prueba de Homoscedasticidad, (Cuesta, 2012) recomienda formar grupos de 4 o 5 residuos consecutivos, para cada grupo calcular promedio y varianza, y posteriormente validar la relación lineal entre promedios de residuos y varianzas de residuos; si se encuentra una relación lineal significativa habrá indicio de Heteroscedasticidad, es decir, que no se estará cumpliendo el supuesto, con la consiguiente revisión y corrección del modelo.
De acuerdo con los criterios establecidos sobre la MSR y las valoraciones realizadas, se considera que:
La MSR resulta una poderosa herramienta de la Modelación Matemático-Estadística, por todo el conjunto de contenidos que incorpora: Algebra matricial, Cálculo Diferencial, Geometría analítica, Investigación Operacional, Diseños de tratamientos y selección de modelos, entre otros aspectos, lo cual resulta de gran apoyo en el desarrollo científico-investigativo de una gran diversidad de ramas de la ciencia.
El empleo de la MSR brinda la posibilidad de determinar condiciones óptimas de los factores que inciden en la respuesta de determinados procesos bajo investigación, con un menor número de tratamientos
En la actualidad se aprecia que la MSR posee un buen apoyo computacional, sobre todo en software libre, que facilita y permite el análisis de los resultados de forma analítica y gráfica.
La MSR se puede utilizar en las condiciones del ámbito agropecuario cubano y otras ramas de ciencia, por las posibilidades que aporta en la planificación y desarrollo de experimentos de tipo factorial completo o fraccionado, en forma secuencial o directa, según la experiencia acumulada sobre los niveles de los factores en análisis y la ubicación de la posible región del punto estacionario.